��Ŀ����
����Ŀ��ij��ѧΪ���˽ⱾУѧ����Ԥ������״����֪ʶ���ռ�������Ӹ�У2000��ѧ���������ȡ�˲���ѧ�����е��飬���������˽�̶ȷ�Ϊ���dz��˽⡱�����˽⡱�����˽���١��������˽⡱���࣬�������˽�����Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش��������⣺

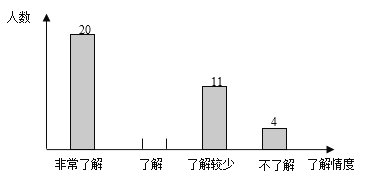
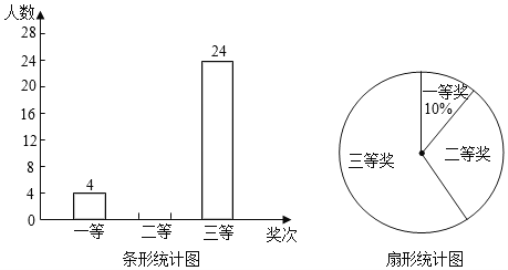
��1�����ε����ѧ�����ж����ˣ�
��2�����Ƹ�У2000��ѧ���С��˽⡱������Լ�ж����ˣ�
��3���������˽⡱��4�����мס�����������������������Ů��������4���������ȡ����ȥ���²μ�Ԥ���¹ڲ�����ʶ��ѵ�����û���״ͼ���б��ķ�������ǡ�ó鵽2�������ĸ���
���𰸡���1��50�ˣ���2��600�ˣ���3��ͼ����������![]()
��������
��1���á����˽⡱���������������ռ�İٷֱȵõ��������������
��2����2000���������С��˽⡱��������ռ�İٷֱȼ��ɣ�
��3������״ͼչʾ����12�ֵȿ��ܵĽ�����ҳ�ǡ�ó鵽2�������Ľ������Ȼ����ݸ��ʹ�ʽ���㣮
��1�����ε����ѧ��������Ϊ4��8%=50�ˣ�
��2�����ε����50��ѧ�����˽��ѧ������ԼΪ50����4+11+20��=15�ˣ�
����Ƹ�У2000��ѧ�������˽���������Լ��2000��![]() =600�ˣ�
=600�ˣ�
��3������״ͼ���£�
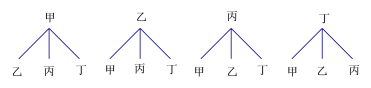
����12�ֿ��ܵĽ�������Ƕ��ǵȿ��ܵģ�ǡ�ó鵽2�������Ľ����2����
��P��ǡ�ó鵽2��������=![]() ��
��
��ǡ�ó鵽2�������ĸ���Ϊ![]() ��
��