Question

【题目】如图，已知抛物线y=﹣ x2+mx+n与x轴交于A （﹣2，0）、B两点，与y轴交于点C．抛物线对称轴为直线x=3，且对称轴与x轴交于点D．

（1）求抛物线的解析式；
（2）点P在线段BC上从点C开始向点B运动（点P不与点B、C重合），速度为每秒 个单位，设运动时间为t（单位：s），过点P作x轴的垂线与抛物线相交于点F．求四边形CDBF的面积S关于t的函数关系式．

Answer 1

【答案】
（1）

∵抛物线对称轴为直线x=3，

∴﹣ ，

∴m= ，

把A（﹣2，0）代入y=﹣ x2+ x+n中，得n=4，

∴抛物线的解析式为y=﹣ x2+ x+4

（2）

易得B（8，0），C（0，4）

设直线BC：y=kx+b，（k≠0）

∴ ，

∴

∴直线BC：y=﹣ x+4，

设点P（p，﹣ p+4），

F（p，﹣ p2+ p+4），

∴ ，

∴S四边形CDBF=S△CDB+S△CBF

=

= ，

在Rt△BCO中，BC= =4 ，

如图，过点P作PG⊥y轴于点G，

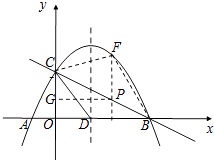
∴PG∥OB

∴△PCG∽△BCO，

∴ ，

∴ ，

∴p=2t

∴S四边形CDBF=﹣4t2+16t+10

【解析】（1）根据对称轴和点A的坐标，直接求出抛物线解析式；（2）先确定出直线BC：y=﹣ x+4，设出点P坐标，表示出FP用面积的和，求出四边形CDBF的面积和点P的横坐标的关系，最后用相似三角形即可．