题目内容
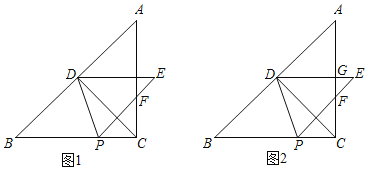
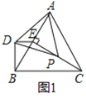
【题目】如图,射线![]() 交一圆于点
交一圆于点![]() ,
,![]() ,射线
,射线![]() 交该圆于点
交该圆于点![]() ,
,![]() ,且
,且![]() .
.
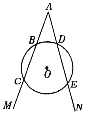
(1)判断![]() 与
与![]() 的数量关系.(不必证明)
的数量关系.(不必证明)
(2)利用尺规作图,分别作线段![]() 的垂直平分线与
的垂直平分线与![]() 的平分线,两线交于点
的平分线,两线交于点![]() (保留作图痕迹,不写作法),求证:
(保留作图痕迹,不写作法),求证:![]() 平分
平分![]() .
.
【答案】(1)AC=AE;(2)图见解析,证明见解析
【解析】
(1)作OP⊥AM,OQ⊥AN于Q,连接AO,BO,DO.证△APO≌△AQO,由BC=DE,得CP=EQ后得证;
(2)同AC=AE得∠ECM=∠CEN,由CE=EF得∠FCE=∠FEC=![]() ∠MCE=
∠MCE=![]() ∠CEN得证.
∠CEN得证.
证明:(1)作OP⊥AM于P,OQ⊥AN于Q,连接AO,BO,DO.

∵![]() ,
,
∴BC=DE,
∴BP=DQ,
又∵OB=OD,
∴△OBP≌△ODQ,
∴OP=OQ.
∴BP=DQ=CP=EQ.
直角三角形APO和AQO中,
AO=AO,OP=OQ,
∴△APO≌△AQO.
∴AP=AQ.
∵CP=EQ,
∴AC=AE.
(2)作图如图所示
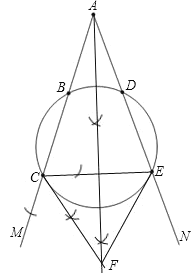
证明:∵AC=AE,∴![]() ,
,
∴![]() , 由于AF是CE的垂直平分线,且CF平分
, 由于AF是CE的垂直平分线,且CF平分![]() ,
,
∴CF=EF.
∴![]()
因此EF平分![]()

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目