题目内容
【题目】如图,已知![]() ,现将直角三角形
,现将直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.


(1)当直角三角形![]() 所放位置如图①所示时,
所放位置如图①所示时,![]() 与
与![]() 存在怎样的数量关系?请说明理由.
存在怎样的数量关系?请说明理由.
(2)当直角三角形![]() 所放位置如图②所示时,请直接写出
所放位置如图②所示时,请直接写出![]() 与
与![]() 之间存在的数量关系.
之间存在的数量关系.
(3)在(2)的条件下,若![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,则
,则![]() 的度数为.
的度数为.
【答案】(1)∠PFD+∠AEM=90°,理由见解析;(2)∠PFD﹣∠AEM=90°;(3)30°.
【解析】
(1)延长MP,交CD于点H,根据AB∥CD得到∠1=∠AEM ,因为∠NPM=90°等量代换即可得出结论,
(2)由题意知:∠AEM=∠PEH,∠PHE=∠BHF,得到∠AEM+∠BHF=90°,再由AB∥CD得到∠PFD+∠BHF=180°,根据等式性质代入即可,
(3)作MQ∥CD,根据AB∥CD∥MQ得∠AEM=∠PMQ,∠QMN=∠MOC,等量代换即可求解.
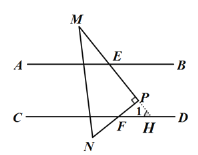
(1)∠PFD+∠AEM=90°,
延长MP,交CD于点H,
∵AB∥CD,
∴∠1=∠AEM ,
∵∠NPM=90°,
∴∠FPH=180°﹣∠NPM=90°,
∵∠1+∠PFD+∠FPH=180°,
∴∠1+∠PFD=90°,
∴∠PFD+∠AEM=90°;
(2)如图:
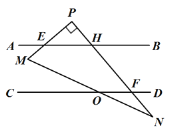
∠PFD﹣∠AEM=90°,
由题意知:∠AEM=∠PEH,∠PHE=∠BHF,
∵∠PEH+∠PHE=90°,
∴∠AEM+∠BHF=90°,
又AB∥CD,
∴∠PFD+∠BHF=180°,
∴∠PFD+∠BHF-(∠AEM+∠BHF)=180°-90°
即∠PFD﹣∠AEM=90°,
(3)30°

作MQ∥CD,
∵AB∥CD,
∴AB∥CD∥MQ,
∴∠AEM=∠PMQ,∠QMN=∠MOC,
∵![]() ,∠DON=∠MOC,
,∠DON=∠MOC,
∴∠PMQ=40°,∠QMN=20°,
∴∠PMN=60°,
又∠P=90°,
∴∠N=90°-60°=30°.

 应用题作业本系列答案
应用题作业本系列答案【题目】九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.