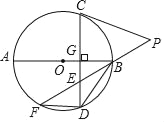
题目内容
【题目】如图,在四边形ABCD中,AB∥CD,∠ECF=∠BCD=90°,CE=CF=5,BC=7,BD平分∠ABC,E是△BCD内一点,F是四边形ABCD外一点.(E可以在△BCD的边上)
(1)求证:DC=BC;
(2)当∠BEC=135°,设BE=a,DE=b,求a与b满足的关系式;
(3)当E落在线段BD上时,求DE的长.

【答案】(1)证明见解析;(2)b2-a2=50;(3)![]() 或
或![]() .
.
【解析】
(1)由角平分线定义得出∠ABD=∠CBD,由平行线的性质得出∠ABD=∠BDC,证出∠CBD=∠BDC,即可得出结论;
(2)证明△DCE≌△BCF(SAS),得出DE=BF,证出△CEF是等腰直角三角形,得出EF= ![]() CE=
CE=![]() ,∠CEF=45°,得出∠BEF=90°,在Rt△BEF中,由勾股定理即可得出结论;
,∠CEF=45°,得出∠BEF=90°,在Rt△BEF中,由勾股定理即可得出结论;
(3)由等腰直角三角形的性质得出BD=![]() BC=
BC=![]() ,∠CBD=∠CDB=45°,同(2)得△DCE≌△BCF(SAS),得出DE=BF,∠CBF=∠CDE=45°,证出∠EBF=90°,BE=BD-DE=
,∠CBD=∠CDB=45°,同(2)得△DCE≌△BCF(SAS),得出DE=BF,∠CBF=∠CDE=45°,证出∠EBF=90°,BE=BD-DE=![]() -DE,在Rt△BEF中,由勾股定理得出方程,解方程即可求出DE.
-DE,在Rt△BEF中,由勾股定理得出方程,解方程即可求出DE.
(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AB∥CD,
∴∠ABD=∠BDC,
∴∠CBD=∠BDC,
∴DC=BC;
(2)解:由(1)得:DC=BC,
∵∠BCD=90°,∠ECF=90°,
∴∠DCE+∠BCE=∠BCF+∠BCE=90°,
∴∠DCE=∠BCF,
在△DCE和△BCF中,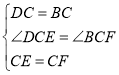 ,
,
∴△DCE≌△BCF(SAS),
∴DE=BF,
∵DE=b,
∴BF=b,
∵∠ECF=90°,CE=CF,
∴△CEF是等腰直角三角形,
∴EF=![]() CE=5
CE=5![]() ,∠CEF=45°,
,∠CEF=45°,
∵∠BEC=135°,
∴∠BEF=90°,
在Rt△BEF中,BE2+EF2=BF2,即a2+(5![]() )2=b2,
)2=b2,
∴b2-a2=50;
(3)解:如图,
∵DC=BC,∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BD=![]() BC=7
BC=7![]() ,∠CBD=∠CDB=45°,
,∠CBD=∠CDB=45°,
同(2)得:△DCE≌△BCF(SAS),
∴DE=BF,∠CBF=∠CDE=45°,
∴∠EBF=∠CBD+∠CBF=45°+45°=90°,
∵BE=BD﹣DE=7![]() ﹣DE,
﹣DE,
∴在Rt△BEF中,EF2=BE2+BF2,即:(5![]() )2=(7
)2=(7![]() ﹣DE)2+DE2,
﹣DE)2+DE2,
解得:DE=4![]() 或DE=3
或DE=3![]() .
.