题目内容
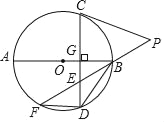
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连结CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)求证:CD=BF;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)连接![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,从而得证;
,从而得证;
(2)连接![]() ,由于
,由于![]() ,
,![]() ,从而可得
,从而可得![]() ,又因为
,又因为![]() ,从而可知
,从而可知![]() ,由于
,由于![]() ,
,![]() ,所以
,所以![]() ,从而得证;
,从而得证;
(3)连接![]() ,易证
,易证![]() ,所以
,所以![]() ,即
,即![]() ,从而可求出
,从而可求出![]() 的长度,再由勾股定理可知
的长度,再由勾股定理可知![]() 的长度,由于
的长度,由于![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,从而可求出
,从而可求出![]() 的值.
的值.
(1)连接BC,
∵BE=DE,
∴∠BDE=∠DBE,
在△BCD与△DFB中,
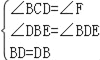
∴△BCD≌△DFB(AAS)
∴CD=BF
(2)连接OC,
∵∠COB=2∠CDB,∠CEB=∠CDB+∠DBE=2∠CDB
∴∠COB=∠CEB,
∵PC=PE,
∴∠COB=∠CEB=∠PCE,
∵AB⊥CD,
∴∠COB+∠OCG=90°,
∴∠PCE+∠OCG=∠PCO=90°,
∴OC⊥CP
∵OC是半径,
∴PC是⊙O的切线,
(3)连接AD,
∵AB是直径,
∴∠ADB=90°,
∵AB⊥CD,
∴![]() =
=![]() ,
,
∴∠BDG=∠A=∠F
∵tan∠F=![]()
∴tan∠A=![]() =
=![]() ,即AG=
,即AG=![]() GD
GD
同理可得:BG=![]() GD,
GD,
∴AG﹣BG=![]() GD﹣
GD﹣![]() GD=
GD=![]()
![]() ,
,
解得:GD=2![]() ,
,
∴CD=2GD=4![]() ,
,
∴BG=![]()
![]()
∴由勾股定理可知:BD=![]()
![]()
∵∠BCD=∠EDB,∠BDC=∠EBD,
∴△BCD∽△EDB
∴![]() =
=![]()
∵BC=BD,
∴ED=![]() =
=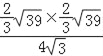 =
=![]()

练习册系列答案
相关题目