Question

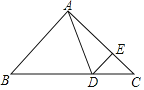
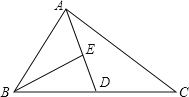
【题目】如图，AD为△ABC的中线，BE为△ABD的中线，

（1）若∠ABE=25°，∠BAD=50°，则∠BED的度数是 度．

（2）在△ADC中过点C作AD边上的高CH．

（3）若△ABC的面积为60，BD=5，求点E到BC边的距离．

Answer 1

【答案】（1）75；（2）作图见解析；（3）点E到BC边的距离为6．

【解析】

（1）根据三角形的一个外角等于与它不相邻的两个内角和，∠BED=∠ABE+∠BAE=75°；
（2）三角形高的基本作法：用圆规以一边两端点为圆心，任意长为半径作两段弧，交于角的两边，再以交点为圆心，用交轨法作两段弧，找到两段弧的交点，连接两个交点，并过另一端点作所成直线的平行线，叫该边所在直线一点，连接该点和另一端点，则为高线；
（3）我们通过证明不难得出三角形中线将三角形分成面积相等的两个三角形，那么可依据D是BC中点，E是AD中点，求出三角形BED的面积．三角形BDE中，E到BD的距离就是BD边上的高，有了三角形BDE的面积，BD的长也容易求得．那么高就求出来了．

（1）∠BED=∠ABE+∠BAE=75°；

（2）

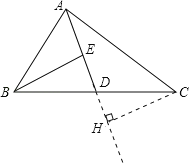
CH为所求的高．

（3）如图，过点E作EF⊥BD于点F，

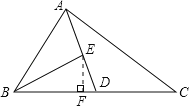
∵AD是BC的中线

∴BD=CD

∴

同理

又∵

∴EF=6

即点E到BC边的距离为6.