题目内容
【题目】如图,在正方形ABCD中,E是CD上一点,DF⊥BE交BE的延长线于点G,交BC的延长线于点F. 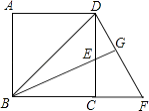
(1)求证:△BCE≌△DCF.
(2)若∠DBE=∠CBE,求证:BD=BF.
(3)在(2)的条件下,求CE:ED的值.
【答案】
(1)解:证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCE=∠DCF=90°,
∴∠CBE﹢∠BEC=90°,
又∵BG⊥DF,
∴∠CBE﹢∠F=90°,
∴∠BEC=∠F,
在△BCE与△DCF中,
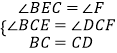 ,
,
∴△BCE≌△DCF(AAS)
(2)解:证明:∵BG⊥DF
∴∠BGD=∠BGF
在△DBG与△FBG中,
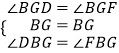 ,
,
∴△DBG≌△FBG(ASA),
∴BD=BF;
(3)解:解:延长AD、BG交于点H.
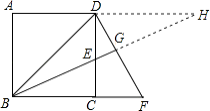
∵BD=BF,BG⊥DF,
∴∠DBG∠FBG,
∵AD∥BC,
∴∠H=∠FBG,
∴∠DBH=∠H,
∴DB=DH,
∵AH∥BC,
∴△BCE∽△HDE,
∴CE:DE=BC:DH,
∴CE:DE=BC:DB.
∵四边形ABCD是正方形,
∴BC:BD=1: ![]() .
.
∴CE:DE=1: ![]() ,
,
∴CE:DE的值为 ![]() .
.
【解析】(1)根据四边形ABCD是正方形可知BC=DC,∠BCE=∠DCF=90°,再由BG⊥DF,可知∠CBE﹢∠F=90°,根据AAS定理即可得出△BCE≌△DCF;(2)根据ASA定理得出△DBG≌△FBG,由全等三角形的性质即可得出结论;(3)延长AD、BG交于点H,由全等三角形的判定定理得出△BCE∽△HDE,再根据相似三角形的对应边成比例即可得出结论.
【考点精析】通过灵活运用正方形的性质和相似三角形的判定与性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案