Question

【题目】如图，正方形AEFG的边AE放置在正方形ABCD的对角线AC上，EF与CD交于点M，得四边形AEMD，且两正方形的边长均为2，则两正方形重合部分（阴影部分）的面积为（ ）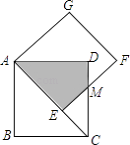
A.﹣4+4
B.4 +4
C.8﹣4
D. +1

Answer 1

【答案】A
【解析】解：∵四边形ABCD是正方形， ∴∠D=90°，∠ACD=45°，AD=CD=2，
则S△ACD= ADCD= ×2×2=2；
AC= AD=2 ，
则EC=2 ﹣2，
∵△MEC是等腰直角三角形，
∴S△MEC= MEEC= （2 ﹣2）2=6﹣4 ，
∴阴影部分的面积=S△ACD﹣S△MEC=2﹣（6﹣4 ）=4 ﹣4．
故选：A．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．