题目内容
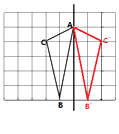
【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线 
成轴对称的△A 
；
（2）线段 
被直线 ；
（3）在直线 上找一点P，使PB+PC的长最短，并算出这个最短长度．
【答案】
（1）解：如图所示：
（2）垂直平分
（3）解：连接BC’交l于点P，如图，在 
BC’D中
∴ 
∴最短长度为5
【解析】（1）根据轴对称图形的性质画出对称轴。
（2）根据轴对称图形的性质可得出结论。
（3）根据作图可知点C和点C’关于直线l对称，因此连接BC’交l于点P，根据直角三角形的勾股定理可以求出线段的长度。
【考点精析】通过灵活运用轴对称的性质和作轴对称图形，掌握关于某条直线对称的两个图形是全等形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上；画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线即可以解答此题．
练习册系列答案
相关题目
