题目内容
【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线![]() :y=x﹣1
:y=x﹣1
(1)求证:点P在直线![]() 上;
上;
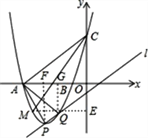
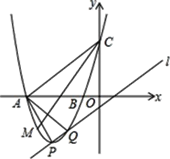
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线![]() 的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标;
(3)若以抛物线和直线![]() 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
【答案】(1)证明见解析;(2)(﹣4,﹣3);(3)m的值为0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
【解析】分析:(1)利用配方法得到y=(x-m)+m-1,点P(m,m-1),然后根据一次函数图象上点的坐标特征判断点P在直线l上;(2)当m= -3时,抛物线解析式为y=x+6x+5,根据抛物线与x轴的交点问题求出A(-5,0),易得C(0,5),通过解方程组![]() 得P(-3,-4),Q(-2,-3),作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,证明Rt△CME∽Rt△PAF,利用相似得
得P(-3,-4),Q(-2,-3),作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,证明Rt△CME∽Rt△PAF,利用相似得![]() ,设M(x,x+6x+5),则
,设M(x,x+6x+5),则![]() ,解得
,解得![]() =0(舍去),
=0(舍去),![]() = -4,于是得到点M的坐标为(-4,-3);(3)通过解方程组
= -4,于是得到点M的坐标为(-4,-3);(3)通过解方程组
![]() 得P(m,m-1),Q(m+1,m),利用两点间的距离公式得到PQ=2,OQ=2m+2m+1,OP=2m-2m+1,然后分类讨论:当PQ=OQ时,2m+2m+1=2;当PQ=OP时,2m-2m+1=2;当OP=OQ时,2m+2m+1=2m-2m+1,再分别解关于m的方程求出m即可.
得P(m,m-1),Q(m+1,m),利用两点间的距离公式得到PQ=2,OQ=2m+2m+1,OP=2m-2m+1,然后分类讨论:当PQ=OQ时,2m+2m+1=2;当PQ=OP时,2m-2m+1=2;当OP=OQ时,2m+2m+1=2m-2m+1,再分别解关于m的方程求出m即可.
本题解析:
(1)证明:∵y=x2﹣2mx+m2+m﹣1=(x﹣m)2+m﹣1,
∴点P的坐标为(m,m﹣1),
∵当x=m时,y=x﹣1=m﹣1,
∴点P在直线l上;
(2)解:当m=﹣3时,抛物线解析式为y=x2+6x+5,
当y=0时,x2+6x+5=0,解得x1=﹣1,x2=﹣5,则A(﹣5,0),
当x=0时,y=x2+6x+5=5,则C(0,5),
可得解方程组![]() ,解得
,解得![]() 或
或![]() ,
,
则P(﹣3,﹣4),Q(﹣2,﹣3),
作ME⊥y轴于E,PF⊥x轴于F,QG⊥x轴于G,如图,
∵OA=OC=5,
∴△OAC为等腰直角三角形,
∴∠ACO=45°,
∴∠MCE=45°﹣∠ACM,
∵QG=3,OG=2,
∴AG=OA﹣OG=3=QG,
∴△AQG为等腰直角三角形,
∴∠QAG=45°,
∵∠APF=90°﹣∠PAF=90°﹣(∠PAQ+45°)=45°﹣∠PAQ,
∵∠ACM=∠PAQ,
∴∠APF=∠MCE,
∴Rt△CME∽Rt△PAF,
∴![]() ,
,
设M(x,x2+6x+5),
∴ME=﹣x,CE=5﹣(x2+6x+5)=﹣x2﹣6x,
∴![]() ,
,
整理得x2+4x=0,解得x1=0(舍去),x2=﹣4,
∴点M的坐标为(﹣4,﹣3);
(3)解:解方程组![]() 得
得![]() 或
或![]() ,则P(m,m﹣1),Q(m+1,m),
,则P(m,m﹣1),Q(m+1,m),
∴PQ2=(m+1﹣m)2+(m﹣m+1)2=2,OQ2=(m+1)2+m2=2m2+2m+1,OP2=m2+(m﹣1)2=2m2﹣2m+1,
当PQ=OQ时,2m2+2m+1=2,解得m1=![]() ,m2=
,m2=![]() ;
;
当PQ=OP时,2m2﹣2m+1=2,解得m1=![]() ,m2=
,m2=![]() ;
;
当OP=OQ时,2m2+2m+1=2m2﹣2m+1,解得m=0,
综上所述,m的值为0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.