Question

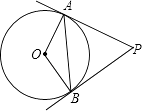
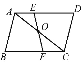
【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )

A. 2 B. 3 C. 4 D. 5

Answer 1

【答案】D

【解析】

由于△ABC与△CDA关于点O对称，那么可得到AB=CD、AD=BC，即四边形ABCD是平行四边形，由于平行四边形是中心对称图形，且对称中心是对角线交点，可根据上述特点对各结论进行判断．

△ABC与△CDA关于点O对称，则AB=CD、AD=BC，所以四边形ABCD是平行四边形，

因此点O就是ABCD的对称中心，则有：

（1）点E和点F；B和D是关于中心O的对称点，正确；

（2）直线BD必经过点O，正确；

（3）四边形ABCD是中心对称图形，正确；

（4）四边形DEOC与四边形BFOA的面积必相等，正确；

（5）△AOE与△COF成中心对称，正确；

其中正确的个数为5个，

故选D．