Question

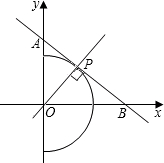已知一次函数的图象过点A（O，3），B（4，O）．
（1）求直线AB的解析式；
（2）作OP⊥直线AB，垂足为点P．
①求垂线段OP的长；
②以点O为圆心，OP为半径作半圆O，请你探究：在x轴的正半轴半圆弧上是否存在一点Q，使得以Q为圆心，r为半径的⊙Q，既与半圆O相切，又与直线OP相交？若存在，试求r的取值范围；若不存在，请说明理由．（可利用备用图解题）

Answer 1

分析：（1）利用一次函数的图象过点A（O，3），B（4，O），由待定系数法求一次函数解析式即可；
（2）①利用三角形面积求出OP的长即可；
②

解答：解：（1）设切线AB直线的解析式为y=kx+b．
∴

b=3 4k+b=0

，
解得：

k=- 3 4 b=3

，
∴y=-

3

4

x+3，
即直线AB的解析式为：y=-

3

4

x+3，

（2）①
∵作OP⊥直线AB，垂足为点P．
∵点A（O，3），B（4，O），∴AO=3，BO=4，
∴AB=5，
∵OP×AB=AO×BO，
∴OP=

AO×BO

AB

=

12

5

，

②

点评：此题难度很大，把一次函数，圆，三角形的知识结合起来，综合性很强，解答此题的关键是根据题意画出图形，利用数形结合求出结论．