题目内容
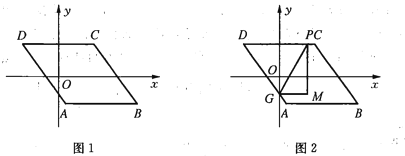
【题目】如图,在![]() 中,
中,![]() ,
,![]() 点
点![]() 在
在![]() 上,
上,![]() 点
点![]() 同时从点
同时从点![]() 出发,分别沿
出发,分别沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,点
匀速运动,点![]() 到达点
到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 向点
向点![]() 运动,点
运动,点![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 也随之停止.在点
也随之停止.在点![]() 运动过程中,以
运动过程中,以![]() 为边作正方形
为边作正方形![]() 使它与
使它与![]() 在线段
在线段![]() 的同铡.设
的同铡.设![]() 运动的时间为
运动的时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() .
.
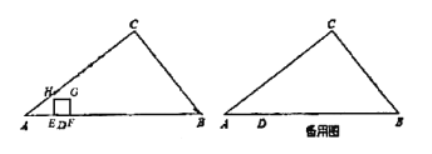
![]() 当
当![]() 时,求正方形
时,求正方形![]() 的顶点刚好落在线段
的顶点刚好落在线段![]() 上时
上时![]() 的值;
的值;
![]() 当
当![]() 时,直接写出当
时,直接写出当![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)①当点![]() 落在线段
落在线段![]() 上时,则
上时,则![]() ,易证△AFG∽△ACB,得出
,易证△AFG∽△ACB,得出![]() ,即
,即![]() ,即可得出结果;
,即可得出结果;
②当点![]() 落在线段
落在线段![]() 时,则
时,则![]() ,易证△AEH∽△ACB,得出
,易证△AEH∽△ACB,得出![]() ,即
,即![]() ,得出结果;
,得出结果;
(2)当t≥2时,△EGB为等腰三角形,则EF=4,由正方形的性质得出EG=![]() EF=4
EF=4![]() ,由题意得出BE=8+2-(t-2)=12-t,BF=8-t,由勾股定理得出BG=
,由题意得出BE=8+2-(t-2)=12-t,BF=8-t,由勾股定理得出BG=![]() ,
,
①当EG=BE时,4![]() =12-t,解得t=12-4
=12-t,解得t=12-4![]() ;
;
②当GE=GB时,4![]() =
=![]() ,解得t=4;
,解得t=4;
③当BE=BG时,12-t=![]() ,解得t=8.
,解得t=8.
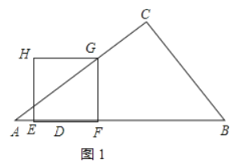
解:![]() ①当点
①当点![]() 落在线段
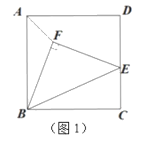
落在线段![]() 上时,如图1所示,
上时,如图1所示,
则![]()
![]()
![]() 即
即![]()
![]()
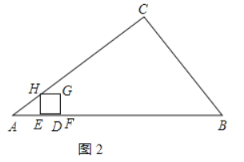
②当点![]() 落在线段
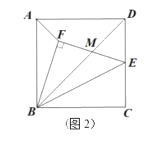
落在线段![]() 时,如图2所示,
时,如图2所示,
则![]() .
.
∵∠AEH=∠ACB=90°,∠A=∠A
∴△AEH∽△ACB.
![]() 即
即![]()
![]()
∴当0<t≤2时,正方形EFGH的顶点刚好落在AG上时t的值为![]() 秒或
秒或![]() 秒.
秒.
故答案为![]() 或
或![]() .
.
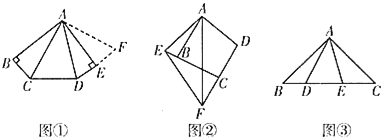
(2)当t≥2时,△EGB为等腰三角形,如图3所示,
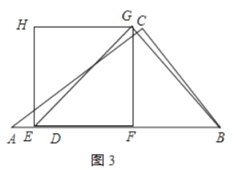
则EF=4
∵四边形EFGH为正方形
∴EG=![]() EF=4
EF=4![]()
由题意得出BE=8+2-(t-2)=12-t,BF=8-t
∴ BG=![]() ,
,
①当EG=BE时,4![]() =12-t
=12-t
解得t=12-4![]() ;
;
②当GE=GB时,4![]() =
=![]()
解得![]() (不合题意,舍去);
(不合题意,舍去);
③当BE=BG时,12-t=![]()
解得t=8.
综上,当t≥2时,△EGB为等腰三角形时t的值为![]() 或4或8
或4或8
故答案为![]()

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案【题目】已知函数![]() (
(![]() 为常数且
为常数且![]() )中,当
)中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .请对该函数及其图像进行如下探究:
.请对该函数及其图像进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量![]() 的取值范围:
的取值范围:
(2)请在下列直角坐标系中画出该函数的图像:
列表如下:
x | … | -4 | -3 | -2 | -1 | 0 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | … |
描点连线:
(3)请结合所画函数图象,写出函数图象的两条性质
(4)请你在上方直角坐标系中画出函数![]() 的图像,结合上述函数的图像,写出不等式
的图像,结合上述函数的图像,写出不等式![]() 的解集.
的解集.