��Ŀ����
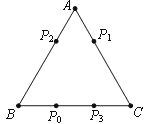
����Ŀ��������̽������ͬ����С��С������ֽƬ������ͼ�ķ�ʽƴ��������
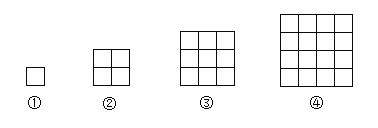
���ɣ��ڢٸ�ͼ������1��С�����Σ�
�ڢڸ�ͼ�αȵڢٸ�ͼ�ζ�3��С�����Σ�
�ڢ۸�ͼ�αȵڢڸ�ͼ�ζ�5��С�����Σ�
����
��(n+1)��ͼ�αȵ�n��ͼ�ζ�________��С��������
�ɷ������½��ۣ���1��1+3+5+��+��2n��1��= ____________��
��2��(n+1)2��n2 = ____________��
��֪ʶ���á�
����һ�����һ�������ü�������������������ʾ�����dz������Ϊ�������������磺9=1+3+5��32=5+7+9+11�����9��32���ǡ���������
�볢�Խ����С������������������ĺͱ�ʾ������
��1��![]() =_____________________________________��
=_____________________________________��
��2��99 =_____________________________________��
���ö�����������Ľ��ۣ������![]() ��ֵ��
��ֵ��
���𰸡� ��2n+1�� n2 2n+1 1+3+5+7+9+11+13 3+5+7+9+11+13+15+17+19 �� 31+33+35
�����������������
������̽����
�ڢڸ�ͼ�αȵڢٸ�ͼ�ζ�3��2��2��1��С�����Σ�
�ڢ۸�ͼ�αȵڢڸ�ͼ�ζ�5��2��3��1��С�����Σ�
����
��n��ͼ�αȵ�n��1��ͼ�ζ�2n��1��С������
��(n��1)��ͼ�αȵ�n��ͼ�ζ�2(n��1)��1��2n��1��С�����Σ�
��1��1��3��5��������2n��1����ʾ��n��ͼ�ε�С�����θ���������1��3��5��������2n��1����n2��
��2��(n��1)2��n2��ʾ��(n��1)��ͼ�αȵ�n��ͼ�ζ��С�����θ���������(n��1)2��n2��2n��1��
��֪ʶ���á�
����һ��
��1�������Ͽ�֪1��3��5��������2n��1����n2����n��7������72��1��3��5��7��9��11��13��
��2��99��100��1
��102��1
��1��3��5������19��1
��3��5������19��
��99��182��152
��(1��3��5������35)��(1��3��5������29)
��31��33��35��
���ö���
��ԭʽÿ�����Ϊһ�飬Ȼ������ǰ�淢�ֵĹ���(n��1)2��n2��2n��1���н�ɣ�
���������
������̽����
��(n��1)��ͼ�αȵ�n��ͼ�ζ� ��2n��1�� ��С��������
�ɷ������½��ۣ���1��1��3��5��������2n��1���� n2 ��
��2��(n��1)2��n2 �� 2n��1 ��
��֪ʶ���á�
����һ��
��1��72�� 1��3��5��7��9��11��13 ��
��2��99 �� 3��5��7��9��11��13��15��17��19 �� 31��33��35 ������һ�ּ��ɣ�
���ö���
����һ����ԭʽ����22��1����(42��32)����62��52����������282��272��
����2��1��1������2��3��1������2��5��1����������2��27��1��
�� 2����1��3��5������27����14
�� 2��196��14
�� 406
����������ԭʽ�� ��22��1����(42��32)����62��52����������282��272��
�� 1��2��3��4��5��6������27��28
�� ![]()
�� 406

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�