题目内容
【题目】在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
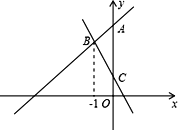
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范围.
【答案】(1)①B(-1,3);k=1;②、1.5;(2)2<k<4.
【解析】试题分析:(1)将点B的横坐标代入y=-2x+1得出点B的纵坐标,将点B的坐标代入y=kx+4求出k的值;根据解析式求出A、C的坐标,然后进行计算;(2)用k的代数式表示点E的横坐标,然后根据不等式求出k的取值.
试题解析:(1)①将x=-1代入y=-2x+1得:y=-2×(-1)+1=3,∴点B的坐标为(-1,3)
将点B的坐标代入y=kx+4得:-k+4=3 解得:k=1
②、根据题意可得:点A的坐标为(0,4) 点C的坐标为(0,1) ∴AC=4-1=3 ∴S=3×1÷2=1.5
(2)当y=0时,x=-![]() 即
即![]() =-
=-![]() 即-2<-
即-2<-![]() <-1 解得:2<k<4.
<-1 解得:2<k<4.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目