题目内容
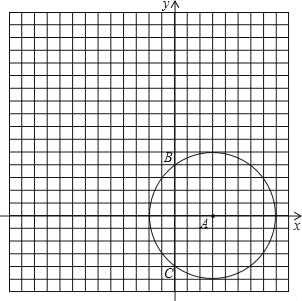
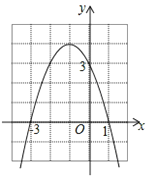
【题目】如图,抛物线y=![]() (x﹣3)2
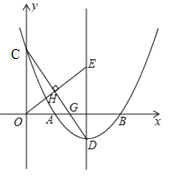
(x﹣3)2![]() 与x轴交于A、B两点(点A在B的左侧),与y轴交于C点,顶点D.
与x轴交于A、B两点(点A在B的左侧),与y轴交于C点,顶点D.
(1)求点A、B、D三点的坐标;
(2)连结CD交x轴于G,过原点O作OE⊥CD,垂足为H,交抛物线对称轴于E,求出E点的纵坐标;
(3)以②中点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标.
【答案】(1)A(3﹣![]() ,0),B(3+
,0),B(3+![]() ,0),D(3,﹣
,0),D(3,﹣![]() );(2)E点的纵坐标为2;(3)P(3+
);(2)E点的纵坐标为2;(3)P(3+![]() ,1).
,1).
【解析】
(1)通过解方程![]() (x﹣3)2
(x﹣3)2![]() =0得A、B两点坐标;利用二次函数性质确定顶点D的坐标;
=0得A、B两点坐标;利用二次函数性质确定顶点D的坐标;
(2)先确定C(0,3),再利用待定系数法求出直线CD的解析式为y=﹣![]() x+3,则可得到G(2,0),抛物线的对称轴与x轴交于M点,如图,则M(3,0),然后证明Rt△OEM∽Rt△DGM,利用相似比求出EM,从而得到E点坐标;
x+3,则可得到G(2,0),抛物线的对称轴与x轴交于M点,如图,则M(3,0),然后证明Rt△OEM∽Rt△DGM,利用相似比求出EM,从而得到E点坐标;
(3)连接PE、EQ,如图,设P(x,![]() (x﹣3)2
(x﹣3)2![]() ),利用切线的性质得PQ⊥EQ,则根据勾股定理得到PQ2=(x﹣3)2+[
),利用切线的性质得PQ⊥EQ,则根据勾股定理得到PQ2=(x﹣3)2+[![]() (x﹣3)2
(x﹣3)2![]() ﹣2]2﹣12,然后进行配方得到PQ2=
﹣2]2﹣12,然后进行配方得到PQ2=![]() [(x﹣3)2﹣5]2+5,从而利用二次函数的性质确定PQ的长最小时点P的坐标.
[(x﹣3)2﹣5]2+5,从而利用二次函数的性质确定PQ的长最小时点P的坐标.
(1)当y=0时,![]() (x﹣3)2
(x﹣3)2![]() =0,解得:x1=3﹣
=0,解得:x1=3﹣![]() ,x2=3+
,x2=3+![]() ,则A(3﹣
,则A(3﹣![]() ,0),B(3+
,0),B(3+![]() ,0);
,0);
抛物线的顶点D的坐标为(3,﹣![]() );
);
(2)当y=0时,y=![]() (x﹣3)2
(x﹣3)2![]() =
=![]() (0﹣3)2
(0﹣3)2![]() =3,则C(0,3),设直线CD的解析式为y=kx+b,把C(0,3),D(3,﹣
=3,则C(0,3),设直线CD的解析式为y=kx+b,把C(0,3),D(3,﹣![]() )代入得:
)代入得: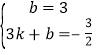 ,解得:
,解得: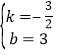 ,∴直线CD的解析式为y=﹣
,∴直线CD的解析式为y=﹣![]() x+3,当y=0时,﹣
x+3,当y=0时,﹣![]() x+3=0,解得:x=2,则G(2,0),抛物线的对称轴与x轴交于M点,如图,则M(3,0).
x+3=0,解得:x=2,则G(2,0),抛物线的对称轴与x轴交于M点,如图,则M(3,0).
∵OE⊥CD,∴∠DHE=90°,∴∠HDE=∠EOM,∴Rt△OEM∽Rt△DGM,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:EM=2,∴E(3,2);
,解得:EM=2,∴E(3,2);
(3)连接PE、EQ,如图,设P(x,![]() (x﹣3)2
(x﹣3)2![]() ).
).
∵PQ为⊙E的切线,∴PQ⊥EQ,∴PQ2=PE2﹣EQ2
=(x﹣3)2+[![]() (x﹣3)2
(x﹣3)2![]() ﹣2]2﹣12
﹣2]2﹣12
=![]() (x﹣3)4﹣
(x﹣3)4﹣![]() (x﹣3)2+
(x﹣3)2+![]()
=![]() [(x﹣3)2﹣5]2+5,当(x﹣3)2﹣5=0,PQ有最小值,此时x=3±
[(x﹣3)2﹣5]2+5,当(x﹣3)2﹣5=0,PQ有最小值,此时x=3±![]() .
.
∵点P在对称轴右侧的抛物线上,∴P点坐标为(3+![]() ,1).
,1).