��Ŀ����
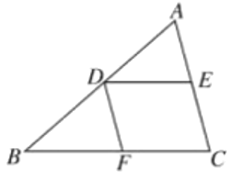
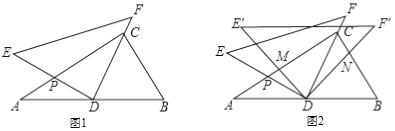
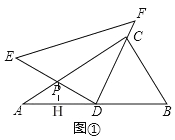
����Ŀ����һ�����dzߣ���Rt��ABC�У���ACB=90�㣬��B=60������Rt��DEF�У���EDF=90�㣬��E=45������ͼ1�ڷţ���DΪAB�ߵ��е㣬DE��AC�ڵ�P��DF������C����BC=2.
��1����֤����ADC����APD��
��2������APD�������
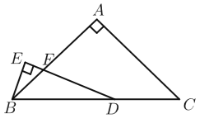
��3����ͼ2������DEF�Ƶ�D˳ʱ�뷽����ת������0�㣼����60��������ʱ�ĵ���ֱ�����dz�Ϊ��DE��F�䣬DE����AC�ڵ�M��DF����BC�ڵ�N�����ж�![]() ��ֵ�Ƿ��������ı仯���仯��������䣬�����
��ֵ�Ƿ��������ı仯���仯��������䣬�����![]() ��ֵ����֮����˵�����ɣ�
��ֵ����֮����˵�����ɣ�
���𰸡�(1)������;(2) ![]() ;(3) �����������ı仯���仯
;(3) �����������ı仯���仯
��������
��1�����жϳ���BCD�ǵȱ������Σ����������ADP=��ACD�����ɵó����ۣ�
��2�����PH������������ε������ʽ���ɵó����ۣ�
��3��ֻҪ֤����DPM����DCN���ƣ��ٸ������������ζ�Ӧ�߳ɱ�������֤����
��1��֤�����ߡ�ABC��ֱ�������Σ���D��AB���е㣬
��AD=BD=CD��
������BCD�У�BC=BD�ҡ�B=60����
���BCD�ǵȱ������Σ�
���BCD=��BDC=60����
���ACD=90������BCD=30����
��ADE=180������BDC����EDF=30����
����ADC����APD����A=��A����ACD=��ADP��
���ADC�ס�APD.
��2���ɣ�1���ѵ���BCD�ǵȱ������Σ���BD=BC=AD=2��
����P��PH��AD�ڵ�H��
�ߡ�ADP=30��=90������B=��A��
��AH=DH=1�� tanA=![]() ��
��
��PH=![]() .
.
���APD�����=![]() AD��PH=
AD��PH=![]()
��3��![]() ��ֵ�����������ı仯���仯.
��ֵ�����������ı仯���仯.
�ߡ�MPD=��A+��ADE=30��+30��=60�������MPD=��BCD=60����
����MPD����NCD����MPD=��NCD=60������PDM=��CDN=����
���MPD�ס�NCD����![]() ��
��
�ɣ�1��֪AD=CD����![]() ��
��
�ɣ�2����֪PD=2AH����PD=![]() ��
��
��![]() ��
��
��![]() ��ֵ�����������ı仯���仯.
��ֵ�����������ı仯���仯.