题目内容
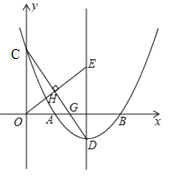
【题目】如图所示是二次函数y=ax2+bx+c的图象.下列结论:①二次三项式ax2+bx+c的最大值为4;②使y≤3成立的x的取值范围是x≤-2;③一元二次方程ax2+bx+c=1的两根之和为-1;④该抛物线的对称轴是直线x=-1;⑤4a-2b+c<0.其中正确的结论有______________.(把所有正确结论的序号都填在横线上)
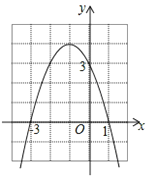
【答案】①④.
【解析】
①由抛物线的顶点坐标为(-1,4),可得出①正确;②由当x=0或x=-2时,y=3,结合抛物线的开口向下,即可得出使y≤3成立的x的取值范围是x≥0或x≤-2,②正确;③由抛物线的对称轴为直线x=-1,可得出一元二次方程ax2+bx+c=1的两根之和为-2,③错误;④根据图象可知,该抛物线的对称轴是直线x=-1,④正确.⑤由x=-2时,![]() ,可得出
,可得出![]() ,⑤错误,综上即可得出结论.
,⑤错误,综上即可得出结论.
①∵抛物线y=ax2+bx+c的顶点坐标为(1,4),
∴二次三项式ax2+bx+c的最大值为4,①正确;
②∵当x=0时,y=3,
∴当x=2时,y=3.
观察函数图象,可知:当x≥0或x≤-2,y≤3, ②错误;
③∵抛物线的对称轴为直线x=1,
∴一元二次方程ax2+bx+c=1的两根之和为2,③错误;
④抛物线的对称轴为直线x=1,④正确.
⑤∵![]() 时,
时,![]() ,
,
∴![]() ,⑤错误.
,⑤错误.
综上所述:正确的结论为①④.
故答案为:①④.

练习册系列答案
相关题目