题目内容
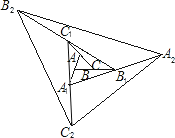
【题目】如图,Rt△ABC中,∠ACB=90°,点M为BA延长线上一点,∠ABC的平分线BE和∠CAM的平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G,则下列结论:①∠APB=45°;②PF=PA;③DG=AP+GH;④BD﹣AH=AB.其中正确的是_____(填序号).

【答案】①②④
【解析】
①正确.证明∠APB=![]() ∠ACB即可.
∠ACB即可.
②正确.证明△PBA≌△PBF(ASA)即可.
③错误.证明DG=AG,GH=GF,AF>AP即可判断.
④正确.根据BD﹣AH=BD﹣DF=BF=AB可得结论.
解:由题意可以假设∠MAP=∠PAC=x,∠ABP=∠PBD=y,
则有![]() ,
,
可得∠APB=![]() ∠ACB=45°,故①正确,
∠ACB=45°,故①正确,
∵PF⊥AD,
∴∠APF=90°,
∴∠APB=∠FPB=45°,
∵PB=PB,∠ABP=∠PBF,
∴△PBA≌△PBF(ASA),
∴PA=PF,BA=BF,故②正确,
∵HP⊥AD,DC⊥AH,
∴AG⊥DH,
∵∠DPF=∠HCF=90°,∠DFP=∠HFC,
∴∠PDF=∠PHA,
∵∠DPF=∠APH=90°,PF=PA,
∴△DPF≌△HPA(AAS),
∴DF=AH,PD=PH,
∴∠PDH=∠AHP=45°,
∴∠ADG=∠DAG=45°,
∴DG=AG,
∵∠GHF=∠GFH=45°,
∴GH=FG,
∵DG=FG+AH=GH+AF,AF>PA,
∴DG≠GH+PA,故③错误,
∵BD﹣AH=BD﹣DF=BF,BF=AB,
∴BD﹣AH=AB,故④正确.
故答案为:①②④.

练习册系列答案
相关题目