题目内容
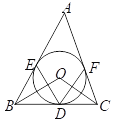
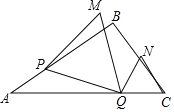
【题目】如图,在△ABC中,AB=7.5,AC=9,S△ABC=![]() .动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
(1)求cosA的值;
(2)当△PQM与△QCN的面积满足S△PQM=![]() S△QCN时,求t的值;
S△QCN时,求t的值;
(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
【答案】(1)coaA=![]() ;(2)当t=
;(2)当t=![]() 时,满足S△PQM=
时,满足S△PQM=![]() S△QCN;(3)当t=
S△QCN;(3)当t=![]() s或
s或![]() s时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
s时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
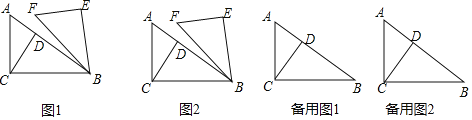
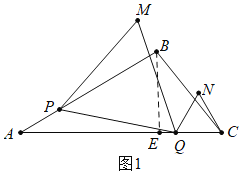
【解析】(1)如图1中,作BE⊥AC于E.利用三角形的面积公式求出BE,利用勾股定理求出AE即可解决问题;
(2)如图2中,作PH⊥AC于H.利用S△PQM=![]() S△QCN构建方程即可解决问题;
S△QCN构建方程即可解决问题;
(3)分两种情形①如图3中,当点M落在QN上时,作PH⊥AC于H.②如图4中,当点M在CQ上时,作PH⊥AC于H.分别构建方程求解即可;
(1)如图1中,作BE⊥AC于E.
∵S△ABC=![]() ACBE=
ACBE=![]() ,
,
∴BE=![]() ,
,
在Rt△ABE中,AE=![]() ,
,
∴coaA=![]() .
.
(2)如图2中,作PH⊥AC于H.
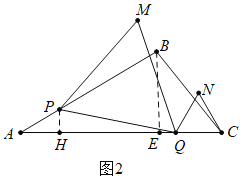
∵PA=5t,PH=3t,AH=4t,HQ=AC-AH-CQ=9-9t,
∴PQ2=PH2+HQ2=9t2+(9-9t)2,
∵S△PQM=![]() S△QCN,
S△QCN,
∴![]() PQ2=
PQ2=![]() CQ2,
CQ2,
∴9t2+(9-9t)2=![]() ×(5t)2,
×(5t)2,
整理得:5t2-18t+9=0,
解得t=3(舍弃)或![]() .
.
∴当t=![]() 时,满足S△PQM=
时,满足S△PQM=![]() S△QCN.
S△QCN.
(3)①如图3中,当点M落在QN上时,作PH⊥AC于H.

易知:PM∥AC,
∴∠MPQ=∠PQH=60°,
∴PH=![]() HQ,
HQ,
∴3t=![]() (9-9t),
(9-9t),
∴t=![]() .
.
②如图4中,当点M在CQ上时,作PH⊥AC于H.

同法可得PH=![]() QH,
QH,
∴3t=![]() (9t-9),
(9t-9),
∴t=![]() ,
,
综上所述,当t=![]() s或
s或![]() s时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
s时,△PQM的某个顶点(Q点除外)落在△QCN的边上.