Question

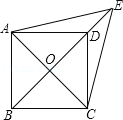
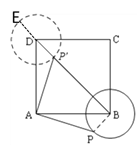
【题目】如右上图，在正方形ABCD中AB=3，，以B为圆心，半径为1画⊙B，点P在⊙B上移动，连接AP，并将AP绕点A逆时针方向旋转 90°至AP′，连接BP′，在点P移动过程中，BP′长的取值范围是______．

Answer 1

【答案】3-1≤BP′≤3+1

【解析】通过画图发现,点P'的运动路线为以D为圆心,以1为半径的圆,可知:当P'在对角线BD上时,最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出的长,而最长距离则是最短距离加上圆的直径即可.

如图，当P′在对角线BD上时，BP′最小，连接BP，

由旋转得：AP=AP′，∠PAP′=90°，
∴∠PAB+∠BAP′=90°，
∵四边形ABCD为正方形，
∴AB=AD，∠BAD=90°，
∴∠BAP′+∠DAP′=90°，
∴∠PAB=∠DAP′，
∴△PAB≌△P′AD，
∴P′D=PB=1，
在Rt△ABD中，∵AB=AD=3，
由勾股定理得：BD=，
∴BP′=BD-P′D=3-1，BE=3-1+2=3+1,

即BP′长度的最小值为（3-1）cm,最长距离为：3+1.

故答案为：3-1≤BP′≤3+1．