题目内容
如图，在等腰梯形ABCD中，AB//CD，AD＝BC，AB＝5，
CD＝2，∠A＝60°，则腰AD的长为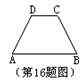
CD＝2，∠A＝60°，则腰AD的长为
3
过C作CE∥AD，可得到平行四边形AECD，从而可求得BE的长，由已知可得到△BCE是等边三角形，此时根据等边三角形的性质来求BC即可．
解：过C作CE∥AD．
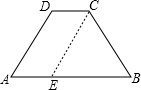
∵等腰梯形ABCD中，AB∥CD，
∴四边形AECD是平行四边形，
∴AE=CD，CE=AD；
又∵AD=BC，
∴EC=BC；
∵AB=5，CD=2，
∴EB=3；
而∠A=∠B，∠A=60°，
∴△BEC是等边三角形；
∴EC=BC=EB，
∴BC=3，
∴AD=3；
故答案是：3．
解：过C作CE∥AD．
∵等腰梯形ABCD中，AB∥CD，
∴四边形AECD是平行四边形，
∴AE=CD，CE=AD；
又∵AD=BC，
∴EC=BC；
∵AB=5，CD=2，
∴EB=3；
而∠A=∠B，∠A=60°，
∴△BEC是等边三角形；
∴EC=BC=EB，
∴BC=3，
∴AD=3；
故答案是：3．
练习册系列答案
阅读快车系列答案
相关题目
，求：BC的长。
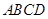的面积为12，
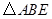是等边三角形，点
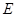在正方形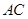
上有一点
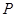，使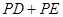
的和最小，则这个最小值为________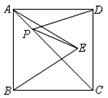
在平面直角坐标系中的位置如图所示，（ ）
，则点
的坐标为
，正方形
（如图2），如此进行下去，正方形
的面积为 ．（用含有n的式子表示，n为正整数）
