题目内容
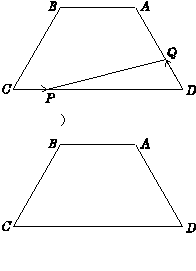
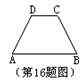
如图，梯形ABCD中，∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P，PH⊥AB于H，若EF=3，PH="1." 则梯形ABCD的面积为___________ 
6
首先根据梯形中位线的性质求得：MN=2PM，EF=
（AD+BC），根据角平分线的性质，求得PM=PH=1，则代入梯形面积公式，即可求得梯形ABCD的面积．
解答：解：过点P作MN⊥BC于M，交AD于N，
∵梯形ABCD中，EF是中位线，
∴AD∥EF∥BC，FD=FC，EF=（AD+BC），
∴PN：PM=FD：FC，
∴PN=PM，
∵PB是∠ABC的平分线，PH⊥AB，
∴PM=PH=1，
∴MN=2PM=2，
∴S梯形ABCD=（AD+BC）?MN=EF?MN=3×2=6．
故答案为：6．
（AD+BC），根据角平分线的性质，求得PM=PH=1，则代入梯形面积公式，即可求得梯形ABCD的面积．解答：解：过点P作MN⊥BC于M，交AD于N，
∵梯形ABCD中，EF是中位线，
∴AD∥EF∥BC，FD=FC，EF=
（AD+BC），∴PN：PM=FD：FC，
∴PN=PM，
∵PB是∠ABC的平分线，PH⊥AB，
∴PM=PH=1，
∴MN=2PM=2，
∴S梯形ABCD=
（AD+BC）?MN=EF?MN=3×2=6．故答案为：6．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
中，AC、BD交于点O，∠ABC=60°,AB=1,E、F分别是线段BO、DO上不与点O重合的点，且BE=DF．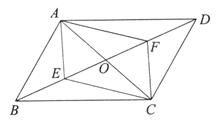
的坐标为
轴，
轴和原点）并写出点
的坐标；
为基本图形，利用轴对称或旋转或平移设计一个图案，说明你的创意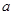
cm，其中矩形的长是宽的2倍，那么它们的面积
、
、
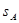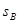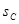之间的关系式正确的是（ ）.
