题目内容
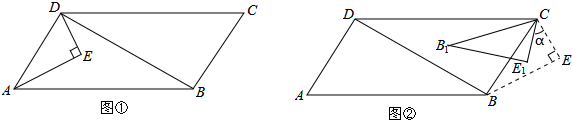
如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°,AB = 6,AD = 9,点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运动到C时,EF与AC重合),把△DEF沿着EF对折,点D的对应点是点G,如图①. 
⑴ 求CD的长及∠1的度数;
⑵ 设DE = x,△GEF与梯形ABCD重叠部分的面积为y.求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
⑶ 当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移,速度为每秒1个单位,当E点移动到线段AB上时运动停止.设平移时间为t(秒),在平移过程中是否存在某一时刻t,使得△ABE为等腰三角形?若存在,请直接写出对应的t的值;若不存在,请说明理由.
(1)CD= 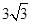 ,∠1 =30°;(2)当x=
,∠1 =30°;(2)当x=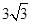 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为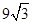 ;(3)存在, t=9或t=9﹣2
;(3)存在, t=9或t=9﹣2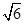 或t=12﹣
或t=12﹣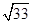 .
.
解析试题分析:(1)过点A作AH⊥BC于点H,构建Rt△AHB和矩形AHCD;通过解直角三角形、矩形的性质求得CD=AH=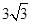 .则
.则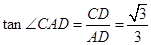 ,故∠CAD=30°;然后由平行线的性质推知∠1=∠CAD=30°;
,故∠CAD=30°;然后由平行线的性质推知∠1=∠CAD=30°;
(2)根据△EFG≌△EFD列出y的表达式,从而讨论x的范围,分别得出可能的值即可;
(3)需要分类讨论:以AB为底和以AB为腰的情况.
试题解析:(1)过点A作AH⊥BC于点H.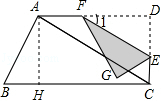
∵在Rt△AHB中,AB=6,∠B=60°,
∴AH=AB•sinB=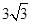
∵四边形ABCD为直角梯形
∴四边形AHCD为矩形
∴CD=AH=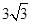 .
.
∵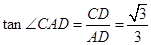
∴∠CAD=30°
∵EF∥AC
∴∠1=∠CAD=30°;
(2)点G恰好在BC上,由对折的对称性可知△FGE≌△FDE,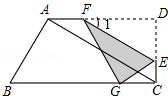
∴GE=DE=x,∠FEG=∠FED=60°
∴∠GEC=60°
∵△CEG是直角三角形
∴∠EGC=30°
∴在Rt△CEG中,EC= EG=
EG= x
x
由DE+EC=CD 得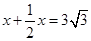
∴x=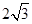 ;
;
当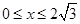 时,
时,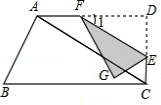
y=S△EGF=S△EDF= ·DE·DF=
·DE·DF= x·
x·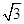 x=
x=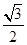 x2,
x2,
∵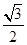 >0,对称轴为y轴
>0,对称轴为y轴
∴当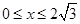 ,y随x的增大而增大
,y随x的增大而增大
∴当x=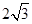 时,y最大值=
时,y最大值= ;
;
当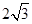 <x≤
<x≤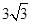 时,设FG,EG分别交BC于点M、N
时,设FG,EG分别交BC于点M、N
∵DE=x,
∴EC=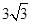 ﹣x,NE=2(
﹣x,NE=2(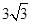 ﹣x),
﹣x),
∴NG=GE﹣NE=3x﹣ .
.
又∵∠MNG=∠ENC=30°,∠G=90°,
∴MG=NG•tan30°=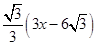 ,
,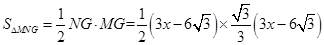
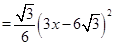 ,
,
y=S△EGF﹣S△MNG=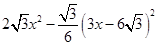 =
=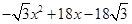 .
.
∵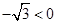 ,对称轴为直线
,对称轴为直线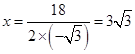 ,
,
∴当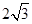 <x≤
<x≤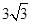 时,y有最大值,
时,y有最大值,
∴当x=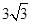 时,
时,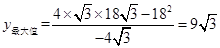 .
.
综合两种情形:由于 <
<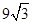
∴当x=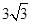 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为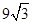 ;
;
(3)由题意可知:AB=6,分三种情况:
①若AE=BE,解得t=9
②若AB=AE,解得t=9﹣2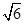
③若BA=BE,解得t=12﹣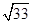 .
.
考点:1.二次函数综合题2.全等三角形的判定与性质.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC


 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=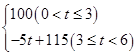
 经过点(3,0),(-1,0).
经过点(3,0),(-1,0).