题目内容
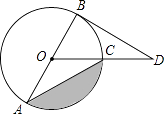
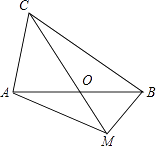
【题目】如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣ ![]() x2+bx+c经过B、D两点.
x2+bx+c经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
【答案】
(1)解:∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1、OA=OC=2,
则点B(2,1)、D(﹣1,2),代入解析式,得:
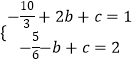 ,
,
解得: 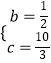 ,
,
∴二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]()
(2)解:如图,
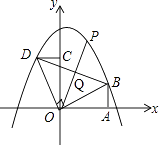
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,
∴DQ=BQ,即点Q为BD的中点,
∴点Q坐标为( ![]() ,
, ![]() ),
),
设直线OP解析式为y=kx,
将点Q坐标代入,得: ![]() k=
k= ![]() ,
,
解得:k=3,
∴直线OP的解析式为y=3x,
代入y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,得:﹣
,得:﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =3x,
=3x,
解得:x=1或x=﹣4,
当x=1时,y=3,
当x=﹣4时,y=﹣12,
∴点P坐标为(1,3)或(﹣4,﹣12)
【解析】(1)由旋转的性质:对应线段相等,求出B、D坐标,代入解析式即可;(2)由旋转性质知OB=OD,直线OP把△BOD的周长分成相等的两部分,可得DQ=BQ,即点Q为BD的中点;中点坐标公式是中点横纵坐标分别是端点横纵坐标和的一半,可求出Q的坐标,求出OQ的解析式,与抛物线解析式联立可求得坐标.

 名校课堂系列答案
名校课堂系列答案【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?