Question

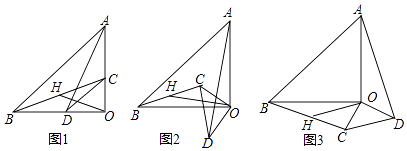
【题目】在Rt△ABC中，∠ACB=90°，点D与点B在AC同侧，∠DAC＞∠BAC，且DA=DC，过点B作BE∥DA交DC于点E，过E作EM∥AC交AB于点M，连结MD.

（1）当∠ADC=80°时，求∠CBE的度数.

（2）当∠ADC=α时:

①求证：BE=CE.

②求证：∠ADM=∠CDM.

③当α为多少度时，DM=EM.

Answer 1

【答案】(1)40°；（2）①见解析，②见解析，③60°

【解析】

（1）根据等腰三角形的性质可得∠ACD的度数，根据∠ACB=90°可求出∠BCE的度数，根据AD//BE可得∠BED=∠ADC=80°，根据三角形外角性质即可求出∠CBE的度数；（2）①由等腰三角形的性质可得∠ACD=90°-，根据∠ACB=90°可得∠BCE=，根据平行线性质可得∠BED=∠ADC=，利用外角性质可求出∠CBE=，即可证明∠BCE=∠CBE，进而可证明BE=CE；②延长EM交AD于F，由EM∥AC可得，进而可得DF=DE，AF=EC=BE，根据AAS可证明△AFM△BEM，可得FM=EM.，根据等腰三角形三线合一即可证明∠ADM=∠CDM；③由②可得DM⊥EM，由可知tan∠DEM=，可得∠DEM=60°，即可求出∠EDM=30°，进而可得=∠ADC=2∠EDM=60°.

（1）∵AD=CD，∠ADC=80°，

∴∠ACD=（180°-80°）=50°，

∵∠ACB=90°，

∴∠BCE=90°-50°=40°，

∵AD//BE，

∴∠BED=∠ADC=80°，

∴∠CBE=∠BED-∠BCE=80°-40°=40°.

（2）①，，

∴

∵AD=CD，

∴∠ACD=（180°-）=90°-，

∵∠ACB=90°，

∴∠BCE=90°-∠ACD= ，

∴∠CBE=∠BED-∠BCE= ，

∴∠CBE=∠BCE，

∴BE=CE.

②延长EM交AD于F

∵，

∴，

∴，

∴AF=EC=BE

∵BE//AD，

∴∠FAM=∠EBM，∠AFM=∠BEM，

∴△AFM△BEM

∴FM=EM.

∴根据三线合一性可得∠ADM=∠CDM

③∵DF=DE，FM=EM，

∴DM⊥EM，

∵DM=EM.

∴tan∠DEM==，

∴∠DEM=60°，

∴∠EDM=30°，

∴=∠ADC=2∠EDM=60°.