题目内容
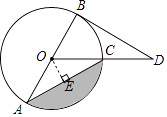
【题目】如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为 . 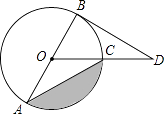
【答案】![]() π﹣4
π﹣4 ![]()
【解析】如图,过O作OE⊥CA于点E,
∵DB为⊙O的切线,
∴∠DBA=90°,
∵∠D=30°,
∴∠BOC=60°,
∴∠COA=120°,
∵OC=OA=4,
∴∠OAE=30°,
∴OE=2,CA=2AE=4 ![]()
∴S阴影=S扇形COA﹣S△COA= ![]() ﹣
﹣ ![]() ×2×4
×2×4 ![]() =
= ![]() π﹣4
π﹣4 ![]() ,
,
故答案为: ![]() π﹣4
π﹣4 ![]() .
.
阴影部分面积等于扇形面积减三角形面积,求三角形面积缺高,因此需要作高,由切线的性质可得∠DBA=90°,由已知∠D=30°可得∠COA=120°,可算出高OE的长,进而算出阴影面积.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
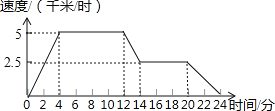
【题目】某天放学后,小敏徒步回家,如图所示,反映了她的速度与时间的变化关系.
(1)请你根据图象填写下表:
时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
速度/(千米/时) |
(2)根据图象或表格你能叙述一下小敏行走的情况吗?