题目内容
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为 . 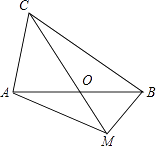
【答案】4 ![]() 或4
或4 ![]() 或4
或4
【解析】如图1,当∠AMB=90°时,
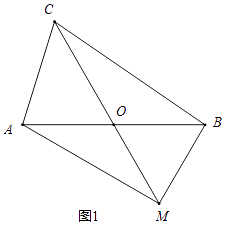
∵O是AB的中点,AB=8,
∴OM=OB=4,
又∵∠AOC=∠BOM=60°,
∴△BOM是等边三角形,
∴BM=BO=4,
∴Rt△ABM中,AM= ![]() =4
=4 ![]() ;
;
如图2,当∠AMB=90°时,
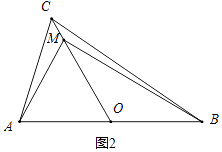
∵O是AB的中点,AB=8,
∴OM=OA=4,
又∵∠AOC=60°,
∴△AOM是等边三角形,
∴AM=AO=4;
如图3,当∠ABM=90°时,

∵∠BOM=∠AOC=60°,
∴∠BMO=30°,
∴MO=2BO=2×4=8,
∴Rt△BOM中,BM= ![]() =4
=4 ![]() ,
,
∴Rt△ABM中,AM= ![]() =4
=4 ![]() ,
,
综上所述,当△ABM为直角三角形时,AM的长为4 ![]() 或4
或4 ![]() 或4.
或4.
所以答案是:4 ![]() 或4
或4 ![]() 或4.
或4.
【考点精析】关于本题考查的等腰三角形的性质和勾股定理的概念,需要了解等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目