题目内容
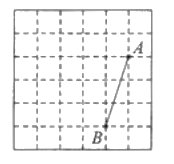
【题目】如图所示,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() .
.
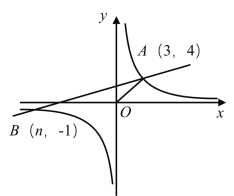
(1)求反比例函数和一次函数的解析式;
(2)在x轴上存在一点C,使![]() 为等腰三角形,求此时点C的坐标;
为等腰三角形,求此时点C的坐标;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ,
,![]() ;(3)-12<x<0或x>3
;(3)-12<x<0或x>3
【解析】
(1)因为反比例函数过A、B两点,所以可求其解析式和n的值,从而知B点坐标,进而求一次函数解析式;
(2)分三种情况:OA=OC,AO=AC,CA=CO,分别求解即可;
(3)根据图像得出一次函数图像在反比例函数图像上方时x的取值范围即可.
解:(1)把A(3,4)代入![]() ,
,
∴m=12,
∴反比例函数是![]() ;
;
把B(n,-1)代入![]() 得n=12.
得n=12.
把A(3,4)、B(-12,1)分别代入y=kx+b中:
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为![]() ;
;
(2)∵A(3,4),△AOC为等腰三角形,OA=![]() ,
,
分三种情况:
①当OA=OC时,OC=5,
此时点C的坐标为![]() ,
,![]() ;
;
②当AO=AC时,∵A(3,4),点C和点O关于过A点且垂直于x轴的直线对称,
此时点C的坐标为![]() ;
;
③当CA=CO时,点C在线段OA的垂直平分线上,
过A作AD⊥x轴,垂足为D,
由题意可得:OD=3,AD=4,AO=5,设OC=x,则AC=x,
在△ACD中,
![]() ,
,
解得:x=![]() ,
,
此时点C的坐标为![]() ;
;
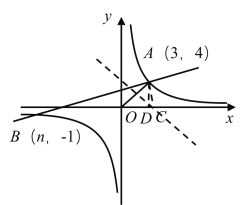
综上:点C的坐标为:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(3)由图得:
当一次函数图像在反比例函数图像上方时,
-12<x<0或x>3,
即使一次函数的值大于反比例函数的值的x的取值范围是:-12<x<0或x>3.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】小云在学习过程中遇到一个函数![]() .下面是小云对其探究的过程,请补充完整:
.下面是小云对其探究的过程,请补充完整:
(1)当![]() 时,对于函数
时,对于函数![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;对于函数
;对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;结合上述分析,进一步探究发现,对于函数
;结合上述分析,进一步探究发现,对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 .
的增大而 .
(2)当![]() 时,对于函数
时,对于函数![]() ,当
,当![]() 时,
时,![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
综合上表,进一步探究发现,当![]() 时,
时,![]() 随
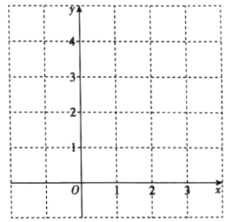
随![]() 的增大而增大.在平面直角坐标系
的增大而增大.在平面直角坐标系![]() 中,画出当
中,画出当![]() 时的函数
时的函数![]() 的图象.
的图象.
(3)过点(0,m)(![]() )作平行于
)作平行于![]() 轴的直线
轴的直线![]() ,结合(1)(2)的分析,解决问题:若直线
,结合(1)(2)的分析,解决问题:若直线![]() 与函数
与函数![]() 的图象有两个交点,则
的图象有两个交点,则![]() 的最大值是 .
的最大值是 .
【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围
的取值范围