题目内容
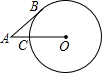如图，AB是⊙O的切线，B为切点，OA交⊙O于点C，已知AB=| 5 |
A、
| ||
| B、1 | ||
| C、2.5 | ||
D、
|
分析：延长AO交⊙O于点D．因为AB是⊙O的切线，B为切点，OA交⊙O于点C，利用切割线定理即有AB2=AC•AD，其中AB=
，OC=2，AD=AC+2+2，代入解之即可．
| 5 |
解答：
解：延长AO交⊙O于点D．
因为AB是⊙O的切线，B为切点，OA交⊙O于点C，
根据切割线定理，得AB2=AC•AD，
∵AB=
，OC=2，AD=AC+2+2，
∴5=AC•（AC+4），
解之得AC=1或AC=-5（舍去），
∴AC=1．
故选B．
解：延长AO交⊙O于点D．因为AB是⊙O的切线，B为切点，OA交⊙O于点C，
根据切割线定理，得AB2=AC•AD，
∵AB=
| 5 |
∴5=AC•（AC+4），
解之得AC=1或AC=-5（舍去），
∴AC=1．
故选B．
点评：本题需利用切割线定理来解决问题．
练习册系列答案
相关题目
12、已知，如图，AB是⊙O的直径，DC切⊙O于点C，AB=2BC，则∠BCD=
如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，过点D作DF⊥AB于点E，交⊙O于点F，OE=1cm，DF=2cm，则CB的长为（ ）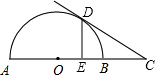
21、如图，AB是⊙O的直径，AC是弦，直线CE和⊙O切于点C，AD⊥CE，垂足为D．求证：AC平分∠BAD．
如图，AB是半圆的直径，直线MN切半圆于点C，AM⊥MN，BN⊥MN，如果AM=a，BN=b，那么半圆的直径为