题目内容
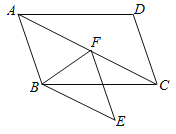
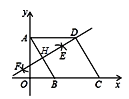
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
A.![]() B.6C.
B.6C.![]() D.
D.![]()
【答案】D
【解析】
连接DB,如图,利用基本作图得到EF垂直平分AB,则DA=DB,再根据菱形的性质得到AD∥BC,AD=AB,则可判断△ADB为等边三角形,所以∠DAB=∠ABO=60°,然后计算出AD=2,![]() ,从而四边形HBCD的周长.
,从而四边形HBCD的周长.
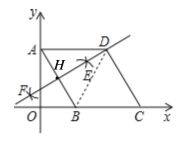
连接DB,如图,
由作法得EF垂直平分AB,
∴DA=DB,AH=BH,
∵四边形ABCD是菱形,
∴AD∥BC,AD=AB,
∴AD=AB=DB,
∴△ADB为等边三角形,
∴∠DAB=60°,
∴∠ABO=60°,
∵A(0,![]() ),
),
∴OA=![]() ,
,
∴OB=![]() OA=1,AB=2OB=2,
OA=1,AB=2OB=2,
∴AD=AB=2,
∴AH=1,
∴![]() ,
,
∴四边形HBCD的周长为:1+2+2+![]() =
=![]() ,
,
故选:D.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目