Question

【题目】已知在同一平面直角坐标系中有函数y1＝ax2﹣2ax+b，y2＝﹣ax+b，其中ab≠0．

（1）求证：函数y2的图象经过函数y1的图象的顶点；

（2）设函数y2的图象与x轴的交点为M，若点M关于y轴的对称点M'在函数y1图象上，求a，b满足的关系式；

（3）当﹣1＜x＜1时，比较y1与y2的大小．

Answer 1

【答案】（1）见解析；（2）b＝﹣a；（3）当a＞0且﹣1＜x＜0时，ax（x﹣1）＞0，y1＞y2；当a＞0且0＜x＜1时，ax（x﹣1）＜0，y1＜y2；当a＜0且﹣1＜x＜0时，ax（x﹣1）＜0，y1＜y2；当a＜0且0＜x＜1时，ax（x﹣1）＞0，y1＞y2．

【解析】

（1）将函数y1的解析式配方，即可找出其顶点坐标，将顶点坐标代入函数y2的解析式中，即可证得结论；
（2）设函数y2的图象与x轴的交点M（m，0），则点M关于y轴的对称点M'（-m，0），根据图象上点的坐标特征得出，解得b=-a；
（3）两函数解析式做差，即可得出y1-y2=ax（x-1），根据x的取值范围可得出x（x-1）的符号，分a＞0或a＜0两种情况考虑，即可得出结论．

（1）证明：∵y1＝ax2﹣2ax+b＝a（x﹣1）2﹣a+b，

∴函数y1的顶点为（1，﹣a+b），

把x＝1代入y2＝﹣ax+b得，y＝﹣a+b，

∴函数y2的图象经过函数y1的图象的顶点；

（2）设函数y2的图象与x轴的交点M（m，0），则点M关于y轴的对称点M'（﹣m，0），

由题意可知，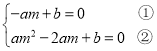

由①得，

代入②得，且ab≠0，

解得b＝﹣a；

（3）∵y1＝ax2﹣2ax+b，y2＝﹣ax+b，

∴y1﹣y2＝ax（x﹣1）．

∵﹣1＜x＜1，

∴当﹣1＜x＜0，x（x﹣1）＞0．当0＜x＜1，x（x﹣1）＜0，当x＝0，x（x﹣1）＝0，

∴y1＝y2；

当a＞0且﹣1＜x＜0时，ax（x﹣1）＞0，y1＞y2；

当a＞0且0＜x＜1时，ax（x﹣1）＜0，y1＜y2；

当a＜0且﹣1＜x＜0时，ax（x﹣1）＜0，y1＜y2；

当a＜0且0＜x＜1时，ax（x﹣1）＞0，y1＞y2．