��Ŀ����
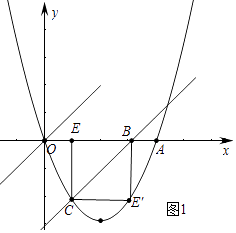
����Ŀ����ͼ1����֪���κ���y=ax2+bx+c��a��b��cΪ������a��0����ͼ�����O��0��0���͵�A��4��0��������ͼ����͵�M��������Ϊ�� ![]() ��ֱ��l�Ľ���ʽΪy=x��
��ֱ��l�Ľ���ʽΪy=x��
��1������κ����Ľ���ʽ��
��2��ֱ��l��x������ƽ�ƣ���ֱ��l�䣬l�����߶�OA�ཻ�ڵ�B����x���·����������ཻ�ڵ�C������C��CE��x���ڵ�E���ѡ�BCE��ֱ��l���۵�������Eǡ�������������ϵ�E��ʱ��ͼ2������ֱ��l��Ľ���ʽ��
��3���ڣ�2���������£�l����y�ύ�ڵ�N���ѡ�BON�Ƶ�O��ʱ����ת135��õ���B��ON�䣬PΪl���ϵĶ��㣬����PB��N��Ϊ����������ʱ������������ĵ�P�����꣮
���𰸡�
��1��
�⣺�����������ߵĶ�������Ϊ��2���� ![]() �����������ߵĽ���ʽΪy=a��x��2��2��
�����������ߵĽ���ʽΪy=a��x��2��2�� ![]() ��
��
�ѣ�0��0������õ�a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() ��x��2��2��
��x��2��2�� ![]() ����y=
����y= ![]() x2��
x2�� ![]() x
x
��2��
�⣺��ͼ1�У���E��m��0������C��m�� ![]() m2��
m2�� ![]() m����B����
m����B���� ![]() m2+
m2+ ![]() m��0����
m��0����
��E�����������ϣ�
��E��B���ڶԳ���Գƣ�
�� ![]() =2��
=2��
���m=1��6����������
��B��3��0����C��1����2����
��ֱ��l��Ľ���ʽΪy=x��3
��3��
�⣺��ͼ2�У�
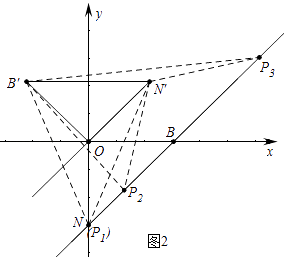
�ٵ�P1��N�غ�ʱ����P1B��N���ǵ��������Σ���ʱP1��0����3����
�ڵ�N��=N��B��ʱ����P��m��m��3����
����m�� ![]() ��2+��m��3��
��2+��m��3�� ![]() ��2=��3
��2=��3 ![]() ��2��
��2��
���m= ![]() ��
�� ![]() ��
��
��P2�� ![]() ��
�� ![]() ����P3��
����P3�� ![]() ��
�� ![]() ����
����
�������������������ĵ�P����Ϊ��0����3���� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ��
��
����������1�������������ߵĶ�������Ϊ��2���� ![]() �����������ߵĽ���ʽΪy=a��x��2��2��
�����������ߵĽ���ʽΪy=a��x��2��2�� ![]() ���ѣ�0��0������õ�a=
���ѣ�0��0������õ�a= ![]() �����ɽ�����⣻��2����ͼ1�У���E��m��0������C��m��
�����ɽ�����⣻��2����ͼ1�У���E��m��0������C��m�� ![]() m2��
m2�� ![]() m����B����
m����B���� ![]() m2+
m2+ ![]() m��0������E��B���ڶԳ���Գƣ��ɵ�
m��0������E��B���ڶԳ���Գƣ��ɵ� ![]() =2���ɴ˼��ɽ�����⣻��3��������������⼴�ɢٵ�P1��N�غ�ʱ����P1B��N���ǵ��������Σ���ʱP1��0����3�����ڵ�N��=N��B��ʱ����P��m��m��3�����г����̽ⷽ�̼��ɣ�
=2���ɴ˼��ɽ�����⣻��3��������������⼴�ɢٵ�P1��N�غ�ʱ����P1B��N���ǵ��������Σ���ʱP1��0����3�����ڵ�N��=N��B��ʱ����P��m��m��3�����г����̽ⷽ�̼��ɣ�
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

����Ŀ��ijУ��ѧ��ȤС����һ����ѧ�����У��������У10��ͬѧ�μӽ������ѧҵˮƽ���Ե������ɼ����õ�������±���ʾ��
�ɼ�/�� | 36 | 37 | 38 | 39 | 40 |
����/�� | 1 | 2 | 1 | 4 | 2 |
����˵����ȷ���ǣ� ��
A.��10��ͬѧ�����ɼ�����λ��Ϊ38��
B.��10��ͬѧ�����ɼ���ƽ����Ϊ38��
C.��10��ͬѧ�����ɼ�������Ϊ39��
D.��10��ͬѧ�����ɼ��ķ���Ϊ2




