题目内容
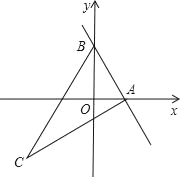
【题目】已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=﹣x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB=![]() .
.
(1)当t=1时,求抛物线的表达式;
(2)试用含t的代数式表示点C的坐标;
(3)如果点C在这条抛物线的对称轴上,求t的值.
【答案】(1)抛物线的表达式为y=﹣x2﹣x+2;(2)点C的坐标为(t﹣4,﹣2t);
(3)t=4﹣![]() .
.
【解析】试题分析:(1)把点A(1,0),B(0,2)分别代入抛物线的表达式,解方程组即可;
(2)如图:作CH⊥x轴,垂足为点H,根据△AOB∽△CHA,得到![]() ,根据tan∠ACB=
,根据tan∠ACB=![]() =
=![]() ,得到
,得到![]() =
=![]() ,根据OA=t,得到点C的坐标为(t-4,-2t).
,根据OA=t,得到点C的坐标为(t-4,-2t).
(3)根据点C(t-4,-2t)在抛物线y=-x2+bx+c的对称轴上,得到t-4=![]() ,即b=2t-8,把点A(t,0)、B(0,2)代入抛物线的表达式,得-t2+bt+2=0,可知t2+(2t-8)t+2=0,即t2-8t+2=0,据此即可求出t的值.
,即b=2t-8,把点A(t,0)、B(0,2)代入抛物线的表达式,得-t2+bt+2=0,可知t2+(2t-8)t+2=0,即t2-8t+2=0,据此即可求出t的值.
试题解析:
(1)∵t=1,y=kx+2,
∴A(1,0),B(0,2),
把点A(1,0),B(0,2)分别代入抛物线的表达式,得![]() ,
,
解得![]() ,
,
∴所求抛物线的表达式为y=﹣x2﹣x+2.
(2)如图:作CH⊥x轴,垂足为点H,得∠AHC=∠AOB=90°,
∵AC⊥AB,
∴∠OAB+∠CAH=90°,
又∵∠CAH+∠ACH=90°,
∴∠OAB=∠ACH,
∴△AOB∽△CHA,
∴![]() ,
,
∵tan∠ACB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=t,OB=2,
∴CH=2t,AH=4,
∴点C的坐标为(t﹣4,﹣2t).
(3)∵点C(t﹣4,﹣2t)在抛物线y=﹣x2+bx+c的对称轴上,
∴t﹣4=![]() ,即b=2t﹣8,
,即b=2t﹣8,
把点A(t,0)、B(0,2)代入抛物线的表达式,得﹣t2+bt+2=0,
∴﹣t2+(2t﹣8)t+2=0,即t2﹣8t+2=0,
解得t=4+![]() ,
,
∵点C(t﹣4,﹣2t)在第三象限,
∴t=4+![]() 不符合题意,舍去,
不符合题意,舍去,
∴t=4﹣![]() .
.

 习题精选系列答案
习题精选系列答案【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
(1)统计表中的a= ,b= ,c= ;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.