题目内容
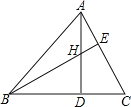
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形;
是矩形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】![]() 证明见解析;(2)
证明见解析;(2)![]()
【解析】
(1)根据平行线求出∠B=∠BAF=90°,∠BCD=∠FDC=45°,根据旋转得出DE=DC,∠EDC=90°,根据等腰三角形性质求出∠AFC=90°,根据矩形的判定即可得出结论;
(2)求出AF和DF,求出DF=EF=1,根据勾股定理求出即可.
(1)∵AD∥BC,AB⊥BC,∠BCD=45°,∴∠B=∠BAF=90°,∠BCD=∠FDC=45°.
∵将CD绕点D逆时针旋转90°至ED,∴DE=DC,∠EDC=90°,∴∠EDF=45°=∠FDC,∴DF⊥CE,∴∠AFC=90°,即∠B=∠BAF=∠AFC=90°,∴四边形ABCF是矩形;
(2)∵四边形ABCF是矩形,∴AF=BC=3,∴DF=3﹣2=1.
∵∠EDF=45°,∠DFE=90°,∴∠DEF=∠EDF=45°,∴DF=EF=1.在Rt△AFE中,由勾股定理得:AE=![]() =
=![]() =
=![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目