Question

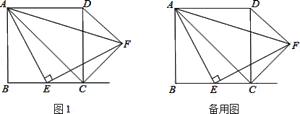
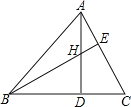
【题目】如图，在△ABC中，高AD和BE交于点H，∠ABC=45°，BE平分∠ABC,下列结论:①∠DAC= 22.5°；②BH= 2CE； ③若连结CH,则CH⊥AB；④若CD=1,则AH=2；其中正确的有( )

A.1个

B.2个

C.3个

D.4个

Answer 1

【答案】C

【解析】

①由同角的余角相等易得∠DAC=∠DBH；②由等腰三角形三线合一可得E为AC中点，再证明△ACD≌△BHD，可得BH=AC，即可判断；③由三角形ABC的三条高交于一点，可知连接CH，则CH⊥AB；④由△ACD≌△BHD得DH=CD=1，HC=，易证HA=HC=，即可判断.

①∵∠ABC=45°，BE平分∠ABC，

∴∠CBE=22.5°，

∵∠DAC+∠ACB=90°，∠CBE+∠ACB=90°，

∴∠DAC=∠CBE=22.5°，

故①正确；

②∵BE平分∠ABC，BE⊥AC，

∴AC=2CE

∵AD⊥BC，∠ABC=45°，

∴∠BAD=∠ABC=45°，

∴AD=BD

在△ACD和△BHD中，

∵∠DAC=∠DBH，AD=BD，∠ADC=∠BDH=90°，

∴△ACD≌△BHD（ASA）

∴AC=BH

∴BH=2CE

故②正确；

③∵H为△ABC两条高的交点，

根据三角形ABC的三条高交于一点，可知连接CH，则CH⊥AB，

故③正确；

④如图，连接CH，

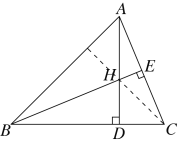
∵△ACD≌△BHD

∴DH=CD=1，

∵HD⊥DC，

∴△CDH为等腰直角三角形，

∴HC=，∠HCD=45°，

又∵∠ECB=90°-∠CBE=67.5°，

∴∠HCA=22.5°=∠HAC

∴HA=HC=

故④错误.

①②③正确，故选C.