题目内容
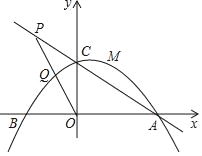
【题目】二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),将二次函数
的左侧),将二次函数![]() 的图象绕点
的图象绕点![]() 旋转180度得到图象为
旋转180度得到图象为![]() ,当
,当![]() 时,图象
时,图象![]() 上点
上点![]() 纵坐标的最小值为
纵坐标的最小值为![]() ,则
,则![]() _________.
_________.
【答案】5
【解析】
根据二次函数解析式可求出A、B两点坐标,设图象G的解析式为y=-x2+bx+c,A点的对应点为A′,根据旋转的性质可求出点A′的坐标,把A′、B坐标代入可求出b、c的值,即可得图象G的解析式,可求出图象G的对称轴,根据二次函数的增减性即可得答案.
∵二次函数y=x2-4x-5的图象与x轴交于A、B两点(点A在点B的左侧),
∴y=0时,x2-4x-5=0,
解得x1=-1,x2=5,
∴A(-1,0),B(5,0),
∵将二次函数y=x2-4x-5的图象绕点B旋转180度得到图象为G,
∴设图象G的解析式为y=-x2+bx+c,A点的对应点为A′,
∴点A′坐标为(11,0),
把B、A′坐标代入y=-x2+bx+c得:![]() ,
,
解得:![]() ,
,
∴图象G点解析式为y=-x2+16x-55=-(x-8)2+9,
∴图象G的对称轴为直线x=8,
∵-1<0,
∴抛物线点开口向下,
∵9-8<8-6,
∴当![]() 时,x=6为函数最小值,
时,x=6为函数最小值,
∴点C纵坐标y=-36+96-55=5,
故答案为:5

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目