题目内容
【题目】如图是某景区每日利润y1(元)与当天游客人数x(人)的函数图像.为了吸引游客,该景区决定改革,改革后每张票价减少20元,运营成本减少800元.设改革后该景区每日利润为y2(元).(注:每日利润=票价收入-运营成本)
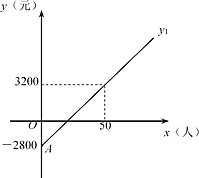
(1)解释点A的实际意义:______.
(2)分别求出y1、y2关于x的函数表达式;
(3)当游客人数为多少人时,改革前的日利润与改革后的日利润相等?
【答案】(1)改革前某景区每日运营成本为2800元;(2)y1=120x-2800;y2=100 x-2000.(3)40人
【解析】
(1)根据题意可得点A的实际意义是改革前某景区每日运营成本为2800元;(2)利用待定系数法即可求出y1关于x的函数表达式;进而根据票价减少20元,运营成本减少800元可得y2关于x的解析式;(3)令y1=y2,列方程求出x的值即可得答案.
(1)改革前某景区每日运营成本为2800元;
(2)设y1与x之间的函数表达式为y1=kx+b(k、b为常数,k≠0),
根据题意,当x=0时,y1=-2800;当x=50时,y1=3200.
所以![]() ,
,
解得![]() ,
,
所以,y1与x之间的函数表达式为y1=120x-2800.
根据题意,y2与x之间的函数表达式为y2=100x-2000.
(3)根据题意,当y1=y2时,得120x-2800=100x-2000.
解得x=40.
答:当游客人数为40人时,改革前的日利润与改革后的日利润相等.

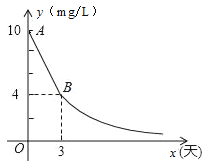
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?