题目内容
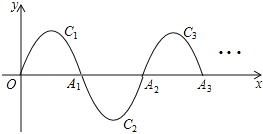
【题目】如图，在平面直角坐标系xOy中，已知抛物线y＝﹣x（x﹣3）（0≤x≤3）在x轴上方的部分，记作C1，它与x轴交于点O，A1，将C1绕点A1旋转180°得C2，C2与x轴交于另一点A2．请继续操作并探究：将C2绕点A2旋转180°得C3，与x轴交于另一点A3；将C3绕点A3旋转180°得C4，与x轴交于另一点A4，这样依次得到x轴上的点A1，A2，A3，…，An，…，及抛物线C1，C2，…，n，…则n的顶点坐标为_____（n为正整数，用含n的代数式表示）．
【答案】
【解析】
根据图形连续旋转，旋转奇数次时，图象在x轴下方，每两个图象全等且相隔三个单位；旋转偶数次时，图象在x轴上方，每两个图象全等且相隔三个单位．
解：这样依次得到x轴上的点A1，A2，A3，…，An，…，及抛物线C1，C2，…，Cn，…．
则Cn的顶点坐标为 （3n﹣
，（﹣1）n+1
），
故答案为：（3n﹣，（﹣1）n+1）．
练习册系列答案
相关题目
