题目内容
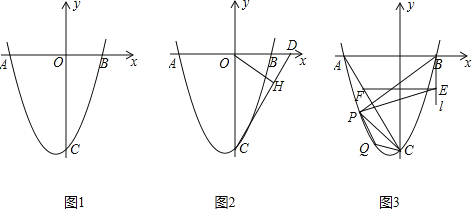
【题目】在平面直角坐标系xOy中,直线y=2x+2与x轴,y轴分别交于点A,B,抛物线y=ax2+bx-![]() 经过点A和点C(4,0).
经过点A和点C(4,0).
(1)求该抛物线的表达式.
(2)连接CB,并延长CB至点D,使DB=CB,请判断点D是否在该抛物线上,并说明理由.
(3)在(2)的条件下,过点C作x轴的垂线EC与直线y=2x+2交于点E,以DE为直径画⊙M,
①求圆心M的坐标;②若直线AP与⊙M相切,P为切点,直接写出点P的坐标.
【答案】(1)![]() ;(2)在,理由见试题解析;(3)①M(0,7);②P(-4,4)或P(3,3).
;(2)在,理由见试题解析;(3)①M(0,7);②P(-4,4)或P(3,3).
【解析】
试题(1)求出A、B的坐标,然后代入抛物线的解析式即可;
(2)过点D作DF垂直x轴于点F,由△CDF∽△CBO得到D的坐标,代入抛物线进行检验;
(3)①先求出E的坐标,设DE与y轴的交点为M′,证明M′就是圆心M,得出M的坐标;
②设P(x,y),则直线PA⊥MA,且MA=5,因为两条直线垂直,它们的k相乘为-1以及两点间距离公式,得到方程组,解方程组即可得到P的坐标.
试题解析:(1)依题意,可知 A(-1, 0),B(0,2),抛物线![]() 经过点A,C (4,0)所以有
经过点A,C (4,0)所以有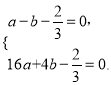 ,解得
,解得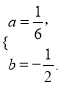 ,∴
,∴![]() ;
;
(2)点D在该抛物线上.依题意,可得BO=2,CO=4.过点D作DF垂直x轴于点F,∴△CDF∽△CBO,∴![]() ,∴DF=4,OF= CF-OC =4,∴ D(-4,4).∵
,∴DF=4,OF= CF-OC =4,∴ D(-4,4).∵![]() ,∴点D在该抛物线上;
,∴点D在该抛物线上;
(3)①由题意可知E(4,10),设DE与y轴的交点为M′,∵M′B∥EC,∴![]() ,∴D M′=EM′,∴M′ 即⊙M的圆心M,∴
,∴D M′=EM′,∴M′ 即⊙M的圆心M,∴![]() ,∴M(0,7).
,∴M(0,7).
②设P(x,y),则直线PA⊥MA,且MA=5,∵直线PA⊥MA,∴ ,解得:
,解得:![]() ,
,![]() ,∴P(-4,4)或P(3,3).
,∴P(-4,4)或P(3,3).


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目