��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+c��x�ύ�ڵ�A����2��0������B��4��0������y�ύ�ڵ�C��0��8��������BC������֪λ��y���Ҳ��Ҵ�ֱ��x��Ķ�ֱ��l����x���������O�˶���B������O���B�㣩���ҷֱ������ߡ��߶�BC�Լ�x���ڵ�P��D��E��
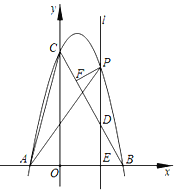
��1���������ߵı���ʽ��
��2������AC��AP����ֱ��l�˶�ʱ����ʹ����PEA����AOC���Ƶĵ�P�����ꣻ
��3����PF��BC������ΪF����ֱ��l�˶�ʱ����Rt��PFD��������ֵ��
���𰸡���1�� y����x2+2x+8����2����P��![]() ������3��
������3��![]()
��������
��1������A��B��C�����������κ�������ʽ��������⣻
��2��ֻ�е���PEA����AOCʱ��PEA����AOC���ɵã�PE��4AE�����P���꣨4k��2��k����������⣻
��3������Rt��PFD��Rt��BOC�ã� ![]() �������PD�����ֵ��������⣮
�������PD�����ֵ��������⣮
�⣺��1������A��B��C�����������κ�������ʽ�ã�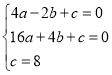 ��
��
��ã�a= -1��b=2��c=8��
�������ߵı���ʽΪ��y����x2+2x+8��
��2���ߵ�A����2��0����C��0��8����
��OA��2��OC��8��
��l��x�ᣬ���PEA����AOC��90����
�ߡ�PAE����CAO��
��ֻ�е���PEA����AOCʱ��PEA����AOC��
��ʱ![]() ������
������![]() ��
��
��AE��4PE��
���P��������Ϊk����PE��k��AE��4k��
��OE��4k��2��
����P���꣨4k��2��k��������κ�������ʽ����ã�
k��0��![]() ����ȥ0�������P��
����ȥ0�������P��![]() ����
����
��3����Rt��PFD����PFD����COB��90����
��l��y�ᣬ
���PDF����COB��
��![]() ��PFD��
��PFD��![]() ��BOC��
��BOC��
��![]() ��
��
��S��PDF��![]() S��BOC��
S��BOC��
��S��BOC��![]() OBOC��
OBOC��![]() ��4��8=16��
��4��8=16��
BC��![]() ��
��
��S��PDF��![]() S��BOC��
S��BOC��![]() PD2��
PD2��
����PDȡ�����ֵʱ��S��PDF���
��B��C�������һ�κ�������ʽ![]() �ã�
�ã�
![]() ��
��
��ã�![]() ��
��
��ֱ��BC�ı���ʽΪ��y����2x+8��
���P��m����m2+2m+8�������D��m����2m+8����
��PD����m2+2m+8+2m��8������m��2��2+4��
��m��2ʱ��PD�����ֵΪ4��
�ʵ�PD��4ʱ����S��PDF��![]() PD2��
PD2��![]() ��
��

����Ŀ��ѧϰһ��Ҫ����������������Ч��Ԥϰ�ɴ���������Ч�ʣ����꼶��1����ѧϰ��ȤС��Ϊ���˽�ȫУ���꼶ѧ����Ԥϰ������Ը�У���꼶ѧ��ÿ��Ŀ�ǰԤϰʱ�䣨��λ��![]() �������˳������飮�������õ������ݷֳ�5�飬������δ��ɵ�Ƶ�������ʷֲ�����Ƶ���ֲ�����ͼ��
�������˳������飮�������õ������ݷֳ�5�飬������δ��ɵ�Ƶ�������ʷֲ�����Ƶ���ֲ�����ͼ��
��� | ��ǰԤϰʱ�� | Ƶ���������� | Ƶ�� |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
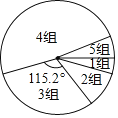
�����ͼ���е���Ϣ���ش��������⣺
��1�����ε������������Ϊ �����е�![]() ��
��![]() ��
��![]() ��
��
��2���Լ����4����������Ӧ������Բ�ĽǵĶ�����
��3����У���꼶����1000��ѧ�����������Щѧ����ÿ���ǰԤϰʱ�䲻����![]() ��ѧ��������
��ѧ��������