Question

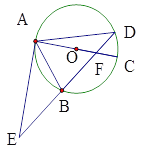
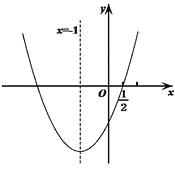
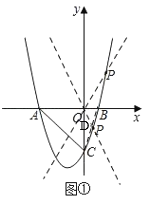
【题目】如图①，抛物线y＝x2﹣（a+1）x+a与x轴交于A、B两点（点A位于点B的左侧），与y轴交于点C．已知△ABC的面积为6．

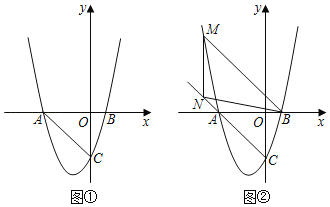
（1）求这条抛物线相应的函数表达式；

（2）在抛物线上是否存在一点P，使得∠POB＝∠CBO，若存在，请求出点P的坐标；若不存在，请说明理由；

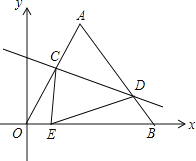
（3）如图②，M是抛物线上一点，N是射线CA上的一点，且M、N两点均在第二象限内，A、N是位于直线BM同侧的不同两点．若点M到x轴的距离为d，△MNB的面积为2d，且∠MAN＝∠ANB，求点N的坐标．

Answer 1

【答案】（1）y＝x2+2x﹣3；（2）存在，点P坐标为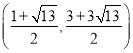或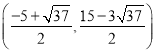；（3）点N的坐标为（﹣4，1）

【解析】

（1）分别令y＝0 ,x＝0,可表示出A、B、C的坐标，从而表示△ABC的面积，求出a的值继而即可得二次函数解析式；

（2）如图①，当点P在x轴上方抛物线上时，平移BC所在的直线过点O交x轴上方抛物线于点P，则有BC∥OP，此时∠POB＝∠CBO，联立抛物线得解析式和OP所在直线的解析式解方程组即可求解；当点P在x轴下方时，取BC的中点D，易知D点坐标为（，），连接OD并延长交x轴下方的抛物线于点P，由直角三角形斜边中线定理可知，OD＝BD，∠DOB＝∠CBO即∠POB＝∠CBO，联立抛物线的解析式和OP所在直线的解析式解方程组即可求解．

（3）如图②，通过点M到x轴的距离可表示△ABM的面积，由S△ABM＝S△BNM，可证明点A、点N到直线BM的距离相等,即AN∥BM，通过角的转化得到AM＝BN，设点N的坐标，表示出BN的距离可求出点N．

（1）当y＝0时，x2﹣（a+1）x+a＝0，

解得x1＝1，x2＝a，

当x＝0，y＝a

∴点C坐标为（0，a），

∵C（0，a）在x轴下方

∴a＜0

∵点A位于点B的左侧，

∴点A坐标为（a，0），点B坐标为（1，0），

∴AB＝1﹣a，OC＝﹣a，

∵△ABC的面积为6，

∴，

∴a1＝﹣3，a2＝4（因为a＜0，故舍去），

∴a＝﹣3，

∴y＝x2+2x﹣3；

（2）设直线BC：y＝kx﹣3，则0＝k﹣3，

∴k＝3；

①当点P在x轴上方时，直线OP的函数表达式为y＝3x，

则，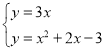

∴，，

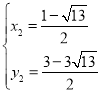∴点P坐标为；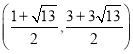

②当点P在x轴下方时，直线OP的函数表达式为y＝﹣3x，

则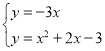

∴，，

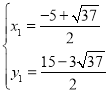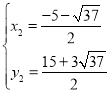∴点P坐标为，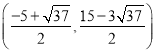

综上可得，点P坐标为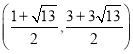或；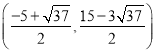

（3）如图，过点A作AE⊥BM于点E，过点N作NF⊥BM于点F，设AM与BN交于点G，延长MN与x轴交于点H；

∵AB＝4，点M到x轴的距离为d，

∴S△AMB＝

∵S△MNB＝2d，

∴S△AMB＝S△MNB，

∴，

∴AE＝NF，

∵AE⊥BM，NF⊥BM，

∴四边形AEFN是矩形，

∴AN∥BM，

∵∠MAN＝∠ANB，

∴GN＝GA，

∵AN∥BM，

∴∠MAN＝∠AMB，∠ANB＝∠NBM，

∴∠AMB＝∠NBM，

∴GB＝GM，

∴GN+GB＝GA+GM即BN＝MA，

在△AMB和△NBM中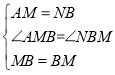

∴△AMB≌△NBM（SAS），

∴∠ABM＝∠NMB，

∵OA＝OC＝3，∠AOC＝90°，

∴∠OAC＝∠OCA＝45°，

又∵AN∥BM，

∴∠ABM＝∠OAC＝45°，

∴∠NMB＝45°，

∴∠ABM+∠NMB＝90°，

∴∠BHM＝90°，

∴M、N、H三点的横坐标相同，且BH＝MH，

∵M是抛物线上一点，

∴可设点M的坐标为（t，t2+2t﹣3），

∴1﹣t＝t2+2t﹣3，

∴t1＝﹣4，t2＝1（舍去），

∴点N的横坐标为﹣4，

可设直线AC：y＝kx﹣3，则0＝﹣3k﹣3，

∴k＝﹣1，

∴y＝﹣x﹣3，

当x＝﹣4时，y＝﹣（﹣4）﹣3＝1，

∴点N的坐标为（﹣4，1）．