��Ŀ����
����Ŀ�����������˹(Apollonius of Perga��Լ��Ԫǰ262-190��)����ϣ����ѧ�ң���ŷ����ã�����������������������Բ�����ۡ��ǹŴ������ԵĿ�ѧ�ɹ�.
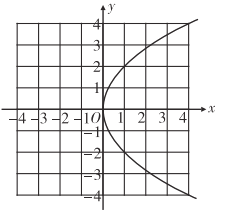
���ϣ���Բ�����ۡ�����������ߵĶ��壺ƽ����һ�����㵽һ��������һ����ֱ�ߵľ���֮�ȵ���1������˵��ƽ����һ���㵽һ������һ��ֱ�ߵľ�����ȵĹ켣����������.
���⣺��֪��![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ������
������![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() �ij���ȣ������
�ij���ȣ������![]() ��
��![]() �Ĺ�ϵʽ.
�Ĺ�ϵʽ.
�⣺��ͼ����![]() ��
��![]() ��
��
��![]()
��![]() ��ֱ��
��ֱ��![]() ��
��
���![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]()
�ߵ�![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() �ij���ȣ�
�ij���ȣ�
��![]() ��
��
ƽ������ã�![]() .
.
��������������![]() �������Ϊ
�������Ϊ![]() ��ֱ��
��ֱ��![]() ��Ϊ
��Ϊ![]() �������������˼·�������
�������������˼·�������![]() ��
��![]() �Ĺ�ϵʽ������ƽ��ֱ������ϵ��������㷨������ͼ�����ܷ���ʲô��
�Ĺ�ϵʽ������ƽ��ֱ������ϵ��������㷨������ͼ�����ܷ���ʲô��
���𰸡�![]() ��ͼ�����������ͼ��Ϊ�������ҵ�������.
��ͼ�����������ͼ��Ϊ�������ҵ�������.
��������
�������⣬�ֱ������![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() �����
�����![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() �ij���ȣ��е÷���
�ij���ȣ��е÷���![]() �����л��ɣ���ƽ��ֱ������ϵ����㡢������.
�����л��ɣ���ƽ��ֱ������ϵ����㡢������.
�⣺��![]() ��
��![]() ��
��
���![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() .
.
�ߵ�![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() �ij���ȣ�
�ij���ȣ�
��![]() .
.
�����![]()
������㷨����ͼ����ͼ��ʾ.
���֣���ͼ��Ϊ�������ҵ�������.

��ϰ��ϵ�д�
�����Ŀ