题目内容
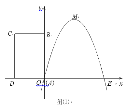
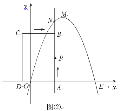
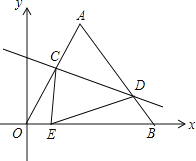
【题目】如图坐标系中,O(0,0),A(3,3![]() ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
A.1:2B.2:3C.6:7D.7:8
【答案】B
【解析】
过A作AF⊥OB于F,如图所示:根据已知条件得到AF=3![]() ,OF=3,OB=6,求得∠AOB=60°,推出△AOB是等边三角形,得到∠AOB=∠ABO=60°,根据折叠的性质得到∠CED=∠OAB=60°,求得∠OCE=∠DEB,根据相似三角形的性质得到BE=OB﹣OE=6﹣
,OF=3,OB=6,求得∠AOB=60°,推出△AOB是等边三角形,得到∠AOB=∠ABO=60°,根据折叠的性质得到∠CED=∠OAB=60°,求得∠OCE=∠DEB,根据相似三角形的性质得到BE=OB﹣OE=6﹣![]() =
=![]() ,设CE=a,则CA=a,CO=6﹣a,ED=b,则AD=b,DB=6﹣b,于是得到结论.
,设CE=a,则CA=a,CO=6﹣a,ED=b,则AD=b,DB=6﹣b,于是得到结论.
过A作AF⊥OB于F,如图所示:
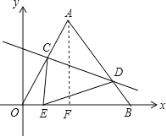
∵A(3,3![]() ),B(6,0),
),B(6,0),
∴AF=3![]() ,OF=3,OB=6,
,OF=3,OB=6,
∴BF=3,
∴OF=BF,
∴AO=AB,
∵tan∠AOB=![]() ,
,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,
∴∠CED=∠OAB=60°,
∵∠OCE+∠COE=∠OCE+60°=∠CED+∠DEB=60°+∠DEB,
∴∠OCE=∠DEB,
∴△CEO∽△EDB,
∴![]() =
=![]() =
=![]() ,
,
∵OE=![]() ,
,
∴BE=OB﹣OE=6﹣![]() =
=![]() ,
,
设CE=a,则CA=a,CO=6﹣a,ED=b,则AD=b,DB=6﹣b,
则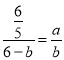 ,
,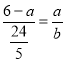 ,
,
∴6b=30a﹣5ab①,24a=30b﹣5ab②,
②﹣①得:24a﹣6b=30b﹣30a,
∴![]() ,
,
即AC:AD=2:3.
故选:B.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目