题目内容
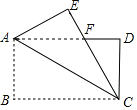
【题目】如图，在四边形ABCD中，AC⊥CD于点C，BD平分∠ADC交AC于点E，∠1=∠2．
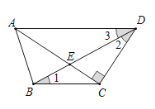
（1） 请完成下面的说理过程．
∵BD平分∠ADC（已知）
∴ （角平分线的定义）
∵∠1=∠2（已知）
∴
∴AD∥BC（ ）
（2）若∠BCE=20°，求∠1的度数．
【答案】（1）∠2=∠3，∠1=∠3，内错角相等，两直线平行；（2）35°
【解析】
（1）根据角平分线的定义，及平行线的判定定理即可求证；
（2）根据平行线的性质定理，可得∠ADC+∠BCD=180°，求得∠ADC度数，由（1）得∠1=∠2=∠3，即可求得∠1度数．
（1）∵BD平分∠ADC（已知）
∴∠2=∠3（角平分线的定义）
∵∠1=∠2（已知）
∴∠1=∠3
∴AD∥BC（内错角相等，两直线平行）
故答案为：∠2=∠3，∠1=∠3，内错角相等，两直线平行
（2）∵AC⊥CD
∴∠ACD=90°
∵∠BCE=20°
∴∠BCD=20°+90°=110°
∵AD∥BC
∴∠ADC+∠BCD=180°
∴∠ADC=180°-110°=70°
∵∠1=∠2=∠3=35°
故答案为：35°
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
