题目内容
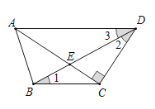
【题目】在△ABC中,∠B=∠C,点D在BC上,点E在AC上,连接DE且∠ADE=∠AED
(1)若∠B=70°,∠ADE=80°,求∠BAD,∠CDE.
(2)当点D在BC(点B,C除外)边上运动时,且点E在AC边上,猜想∠BAD与∠CDE的数量关系是,并证明你的猜想.

(3)当点D在BC(点B,C除外)边上运动时,且点E在AC边上,若∠BAD=25°,求∠CDE.

【答案】(1)20°;10°(2)∠BAD=2∠CDE,理由见解析(3)12.5°
【解析】
(1)根据等腰三角形的性质求出∠BAC,∠DAE,即可求出∠BAD,再根据外角定理求出∠CDE;
(2)设B=a,∠ADE=b,同(1)理即可求解;
(3)利用(2)的结论即可求解.
(1)∵∠B=∠C=70°,∠ADE=∠AED=80°
∴∠BAC=180°-(∠B+∠C)=40°,∠DAE=180°-(∠ADE +∠AED)=20°,
∴∠BAD=∠BAC-∠DAE=20°,
∵∠AED是△DCE的一个外角,
∴∠CDE=∠AED-∠C=10°;
(2)设∠B=∠C=a,∠ADE=∠AED=b
∴∠BAC=180°-(∠B+∠C)=180°-2a,∠DAE=180°-(∠ADE +∠AED)=180°-2b,
∴∠BAD=∠BAC-∠DAE=(180°-2a)- (180°-2b)=2(a-b)
∵∠AED是△DCE的一个外角,
∴∠CDE=∠AED-∠C= a-b ;
∴∠BAD=2∠CDE
(3)∵∠BAD=2∠CDE,∠BAD=25°,
∴∠CDE=![]() ∠BAD=12.5°.
∠BAD=12.5°.

练习册系列答案
相关题目