题目内容
【题目】如图,在半径为2的⊙O中,弦AB长为2.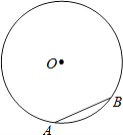
(1)求点O到AB的距离.
(2)若点C为⊙O上一点(不与点A,B重合),求∠BCA的度数.
【答案】
(1)解:过点O作OD⊥AB于点D,连接AO,BO.如图1所示: 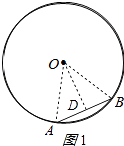
∵OD⊥AB且过圆心,AB=2,
∴AD= ![]() AB=1,∠ADO=90°,
AB=1,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=2,AD=1,
∴OD= ![]() =
= ![]() .
.
即点O到AB的距离为 ![]() .
.
(2)解:如图2所示: 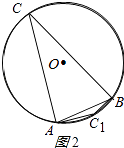
∵AO=BO=2,AB=2,
∴△ABO是等边三角形,
∴∠AOB=60°.
若点C在优弧 ![]() 上,则∠BCA=30°;
上,则∠BCA=30°;
若点C在劣弧 ![]() 上,则∠BCA=
上,则∠BCA= ![]() (360°﹣∠AOB)=150°;
(360°﹣∠AOB)=150°;
综上所述:∠BCA的度数为30°或150°.
【解析】(1)根据题意得到∠ADO=90°,根据勾股定理求出OD的值,即点O到AB的距离;(2)根据题意得到△ABO是等边三角形,∠AOB=60°,根据圆周角与圆心角的关系求出∠BCA的度数为30°或150°.
【考点精析】掌握圆周角定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目