��Ŀ����
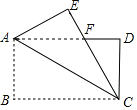
����Ŀ����ͼ��������ֽƬABCD�У�AB=4��BC=6������ABC��AC�۵���ʹ��B���ڵ�E����CE��AD�ڵ�F�����AFC���������___��
���𰸡�![]()
��������
�ɾ��ε����ʿɵ�AB=CD=4��BC=AD=6��AD//BC����ƽ���ߵ����ʺ��۵������ʿɵá�DAC=��ACE���ɵ�AF=CF���ɹ��ɶ�������AF�ij����������AFC�������
�⣺![]() �ı���ABCD�Ǿ���
�ı���ABCD�Ǿ���
![]() ��
��![]() ��
��![]()
![]() ��
��
![]() �۵�
�۵�
![]() ��
��
![]()
![]()
��![]() ��
��![]() ��
��
![]() ��
��
![]()
![]() .
.
�ʴ�Ϊ��![]() .
.
���㾦��
���⿼���˷��۱任�����ε����ʣ����ɶ��������ù��ɶ�����AF�ij��DZ���Ĺؼ���
�����͡������
��������
12
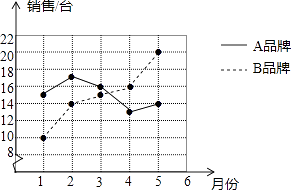
����Ŀ��ij��˾Ҫ��Ƹһ���µĴ�ѧ������˾����Χ�ļס���������ѡ�˽�����������ԣ��ɼ������ʾ������ʵ����Ҫ���涨���������ܡ�ѧҵ������Ե÷ְ�5��3��2�ı���ȷ�����˵IJ��Գɼ����÷�����߱�¼ȡ����ʱ______����¼ȡ��
�÷� | ���� | ���� | ѧҵ |
�� | 95 | 84 | 61 |
�� | 87 | 80 | 77 |
���𰸡���
��������
��������ͱ����е����ݿ��Էֱ���ü�����λѡ�ֵijɼ����Ӷ����Խ���⣮
�⣺�������ͼ���ɵã�
��ƽ���ɼ�![]() ��
��
�ҵ�ƽ���ɼ�![]() ��
��
![]() ��
��
�ʼ�ѡ�ֵ÷ָߣ�
�ʴ�Ϊ���ף�

��ϰ��ϵ�д�
 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
�����Ŀ