题目内容
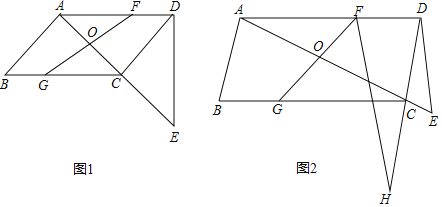
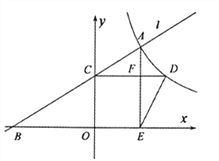
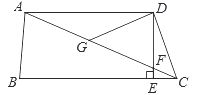
【题目】操作发现:如图1,Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,过点D作DE⊥BC,交AB于点E,在EB上截取EF=AE,过点F作FG⊥AC于点G,GF与ED相交于点H,且点H恰好为GF的中点,连接DG,DF.
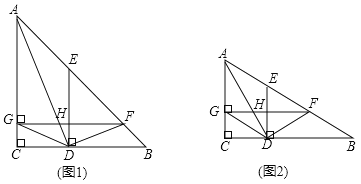
(1)小明发现△GCD≌△DHF,请你写出证明过程;
(2)小亮同学经过探究发现:AF=AC+GC.请你帮助小亮同学证明这一结论.
特例探究:
(3)如图2,若∠B=30°,探究四边形AGDE是哪种特殊的四边形,并说明理由.
【答案】(1)见解析;(2)见解析;(3)四边形AGDE是菱形,见解析.
【解析】
(1)利用角平分线与垂直的性质得到AC∥ED,得到∠BAD=∠ADE,根据平行得到∠CDG=∠DGF,从而求出∠FHD=∠C=90°,再根据垂直平分线性质得到DG=DF,∠DFG=∠DGF,故∠CDG=∠DFG,再根据AAS即可证明全等三角形;
(2)过D作DP⊥AB于P,根据AD平分∠CAB,DC⊥AC,得到DC=DP,故可证得Rt△CAD≌Rt△PAD,得到AC=AP,又GD=FD,DC=PD,得到Rt△GCD≌Rt△FPD
故CG=PF,即可求出AF=AP+PF=AC+GC;
(3)根据∠B=30°,FG∥BC,得到∠AFG=30°,得到AG=![]() AF,AG=AE,根据两组对边相等得到四边形AGDE是平行四边形,再由AG=AE,得到四边形AGDE是菱形.
AF,AG=AE,根据两组对边相等得到四边形AGDE是平行四边形,再由AG=AE,得到四边形AGDE是菱形.
证明:(1)∵AD平分∠CAB,
∴∠CAD=∠BAD,
∵DE⊥BC,∠C=90°,
∴∠EDB=∠C=90°,
∴AC∥ED,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=ED,∵FG⊥AC,
∴∠AGF=∠C=90°,
∴FG∥BC,
∴∠CDG=∠DGF,
∵AC∥ED,FG⊥AC,
∴FG⊥ED,∴∠FHD=90°,
∵点H恰好为GF的中点,
∴ED是线段GF的垂直平分线,
∴DG=DF,∠DFG=∠DGF,
∴∠CDG=∠DFG,
在△GDC与△DFH中,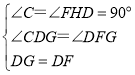 ,
,
∴△GDC≌△DFH(AAS);
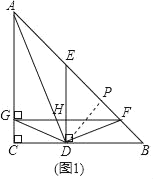
(2)过D作DP⊥AB于P,
∵AD平分∠CAB,DC⊥AC,
∴DC=DP,
在Rt△CAD与Rt△PAD中![]() ,
,
∴Rt△CAD≌Rt△PAD(HL),
∴AC=AP,
∵GD=FD,DC=PD,
∴Rt△GCD≌Rt△FPD(HL),
∴CG=PF,
∴AF=AP+PF=AC+GC;
(3)四边形AGDE是菱形,
理由:∵∠B=30°,FG∥BC,
∴∠AFG=30°,
∴AG=![]() AF,
AF,
∴AG=AE,
∵AG∥ED,AE=DE,
∴AG=ED,
∴四边形AGDE是平行四边形,
∵AG=AE,
∴四边形AGDE是菱形.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案